Distribución binomial
En el ejercicio anterior, modelaste los ensayos de Bernoulli. La distribución binomial es la suma del número de resultados exitosos en un conjunto de ensayos de Bernoulli.
La notación de la distribución binomial es \(B(n, p)\), donde \(n\) es el número de experimentos y \(p\) es la probabilidad de éxito.
Para este ejercicio, considera 10 lanzamientos consecutivos de una moneda justa. Has apostado por caras y consideras este resultado de un lanzamiento como un éxito.
Recuerda que:
dbinom(x = k, size = n, prob = p)calcula \(P(X = k)\) para \(X \sim B(n, p)\),pbinom(q = k, size = n, prob = p)calcula \(P(X \le k)\) para \(X \sim B(n, p)\).
Recuerda que para distribuciones discretas que toman valores enteros: \(P(X \ge k) = 1 - P(X \le k-1)\).
Por ejemplo:
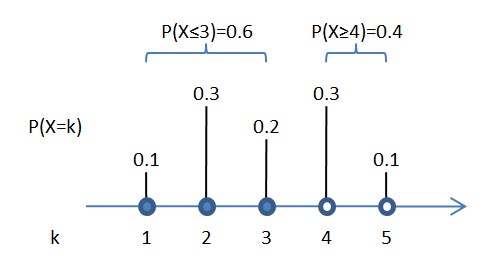
Así, \(P(X \ge 4) = 1 - P(X \le 3)\).
Este ejercicio forma parte del curso
Practicing Statistics Interview Questions in R
Instrucciones del ejercicio
- Asigna la probabilidad de obtener exactamente 6 caras a
six_tailse imprime el resultado. - Asigna la probabilidad de obtener 7 caras o menos a
seven_or_lesse imprime el resultado. - Asigna la probabilidad de obtener 5 caras o más a
five_or_moree imprime el resultado.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# The probability of getting 6 tails
six_tails <- ___(___ = ___, size = ___, prob = ___)
print(six_tails)
# The probability of getting 7 or less tails
seven_or_less <- ___(___ = ___, size = ___, prob = ___)
print(seven_or_less)
# The probability of getting 5 or more tails
five_or_more <- 1 - ___(___ = ___, size = ___, prob = ___)
print(five_or_more)