Distribuição binomial
No exercício anterior, você modelou os ensaios de Bernoulli. A distribuição binomial é a soma do número de sucessos em um conjunto de ensaios de Bernoulli.
A notação da distribuição binomial é \(B(n, p)\), em que \(n\) é o número de experimentos e \(p\) é a probabilidade de sucesso.
Para este exercício, considere 10 lançamentos consecutivos de uma moeda justa. Você apostou em coroa e considera esse resultado de um lançamento como um sucesso.
Lembre-se de que:
dbinom(x = k, size = n, prob = p)calcula \(P(X = k)\) para \(X \sim B(n, p)\),pbinom(q = k, size = n, prob = p)calcula \(P(X \le k)\) para \(X \sim B(n, p)\).
Lembre-se de que, para distribuições discretas que assumem números inteiros: \(P(X \ge k) = 1 - P(X \le k-1)\).
Por exemplo:
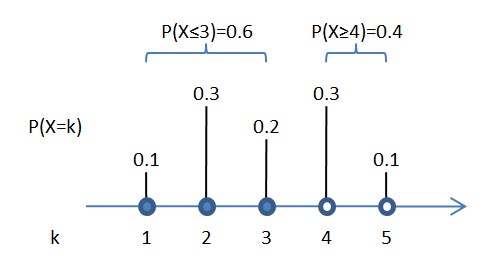
Assim, \(P(X \ge 4) = 1 - P(X \le 3)\).
Este exercício faz parte do curso
Praticando perguntas de entrevista de Estatística em R
Instruções do exercício
- Atribua a probabilidade de obter exatamente 6 coroas a
six_tailse imprima o resultado. - Atribua a probabilidade de obter 7 coroas ou menos a
seven_or_lesse imprima o resultado. - Atribua a probabilidade de obter 5 coroas ou mais a
five_or_moree imprima o resultado.
Exercício interativo prático
Experimente este exercício completando este código de exemplo.
# The probability of getting 6 tails
six_tails <- ___(___ = ___, size = ___, prob = ___)
print(six_tails)
# The probability of getting 7 or less tails
seven_or_less <- ___(___ = ___, size = ___, prob = ___)
print(seven_or_less)
# The probability of getting 5 or more tails
five_or_more <- 1 - ___(___ = ___, size = ___, prob = ___)
print(five_or_more)