Optimisation de la production : Score & Rank

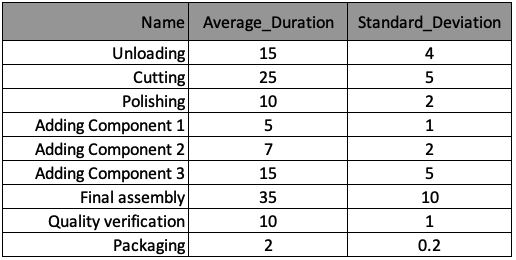
Utilisons le même modèle à événements discrets de l’usine d’horloges murales et mettons en place une routine d’optimisation « Score & Rank ». Pour votre confort, le processus de fabrication est à nouveau résumé dans le tableau ci-dessous. Les informations ont été stockées dans une liste de dictionnaires nommée processes, avec un dictionnaire par processus. Les clés de ce dictionnaire correspondent aux en-têtes de colonnes du tableau.

Table with process names and their duration statistics, namely mean and standard deviation.

La méthode plot_results() utilisée pour générer les graphiques dans cet exercice a été préchargée et est présentée ci-dessous.

def plot_results(objective_func):
    # Score
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.scatterplot(ax=axes[p], x=process_duration_all[:, p], y=objective_func, c=objective_func, cmap="turbo_r")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Duration [min]", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Objective function score")
    plt.show()

    # Rank
    index_sort = np.argsort(objective_func)
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.lineplot(ax=axes[p], x=np.linspace(0, NUM_SIMULATIONS, NUM_SIMULATIONS),
                     y=process_duration_all[index_sort, p], color="orchid")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Score-ranked scenarios", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Duration [min]")
    plt.show()

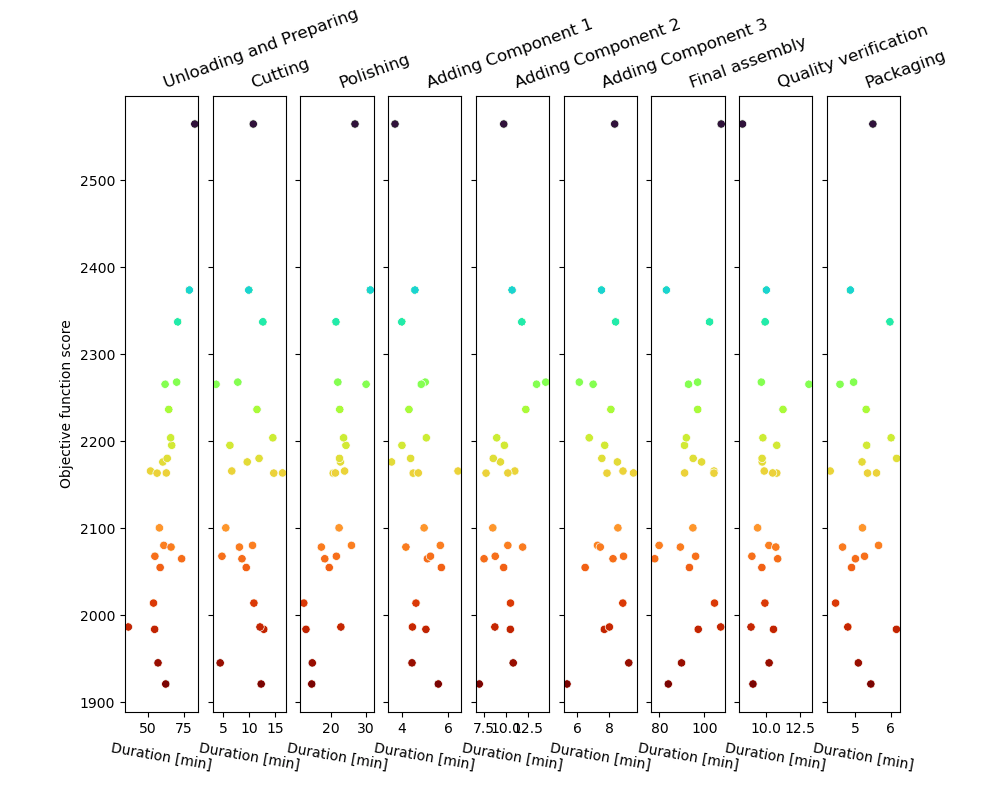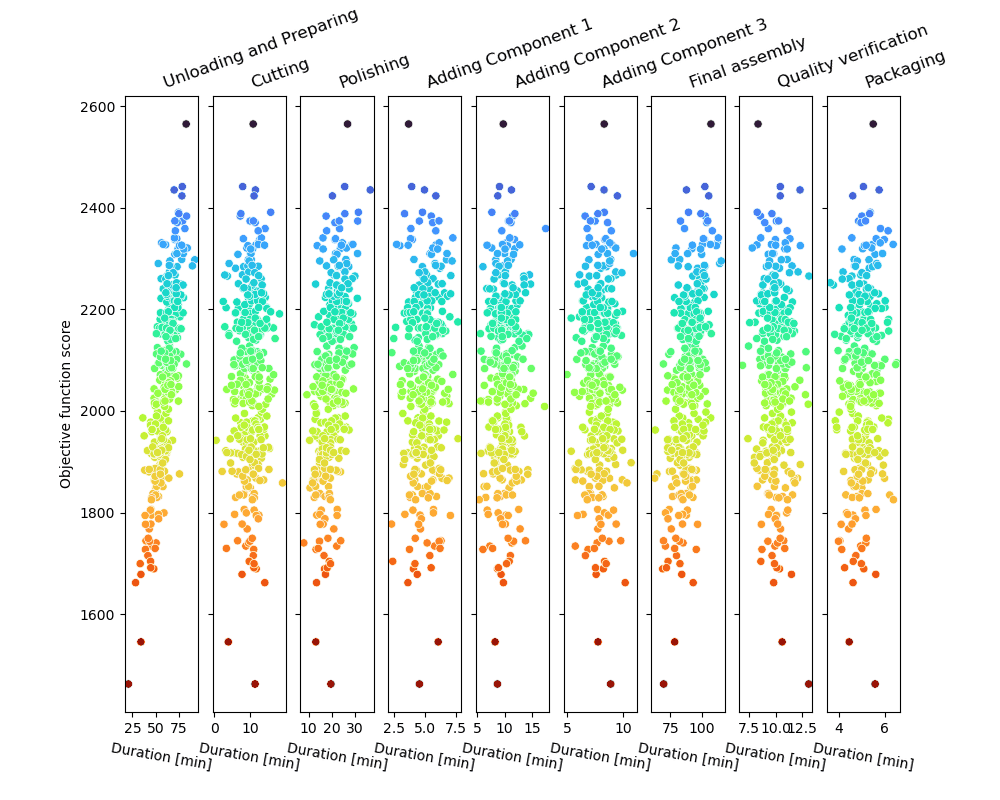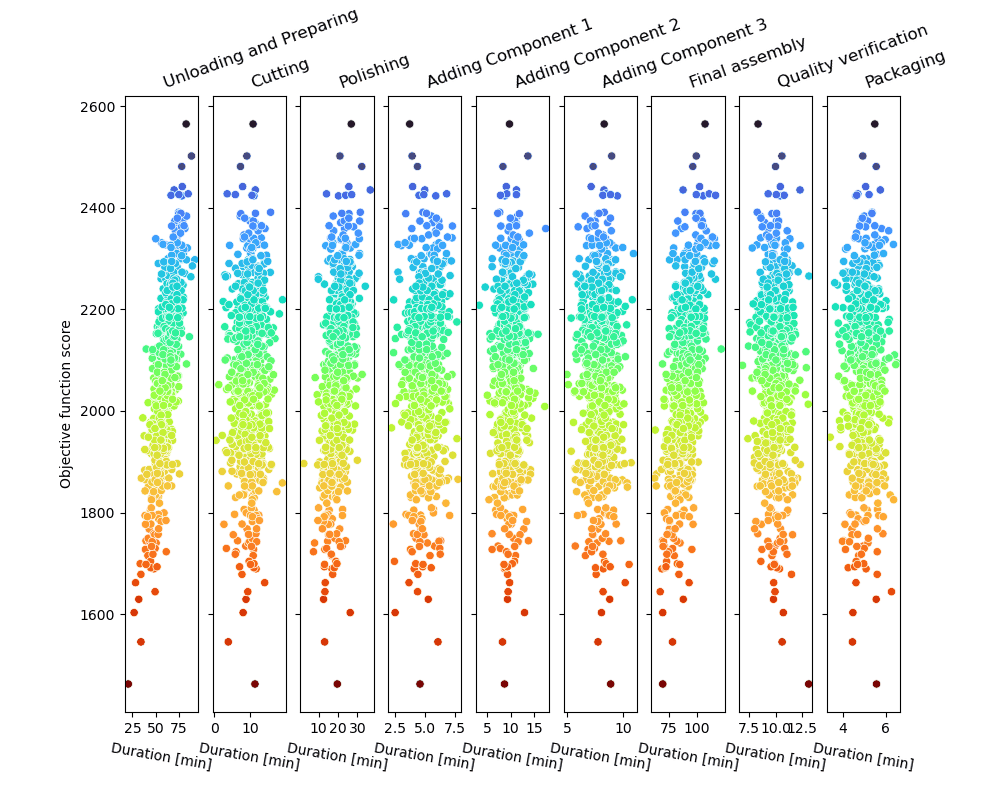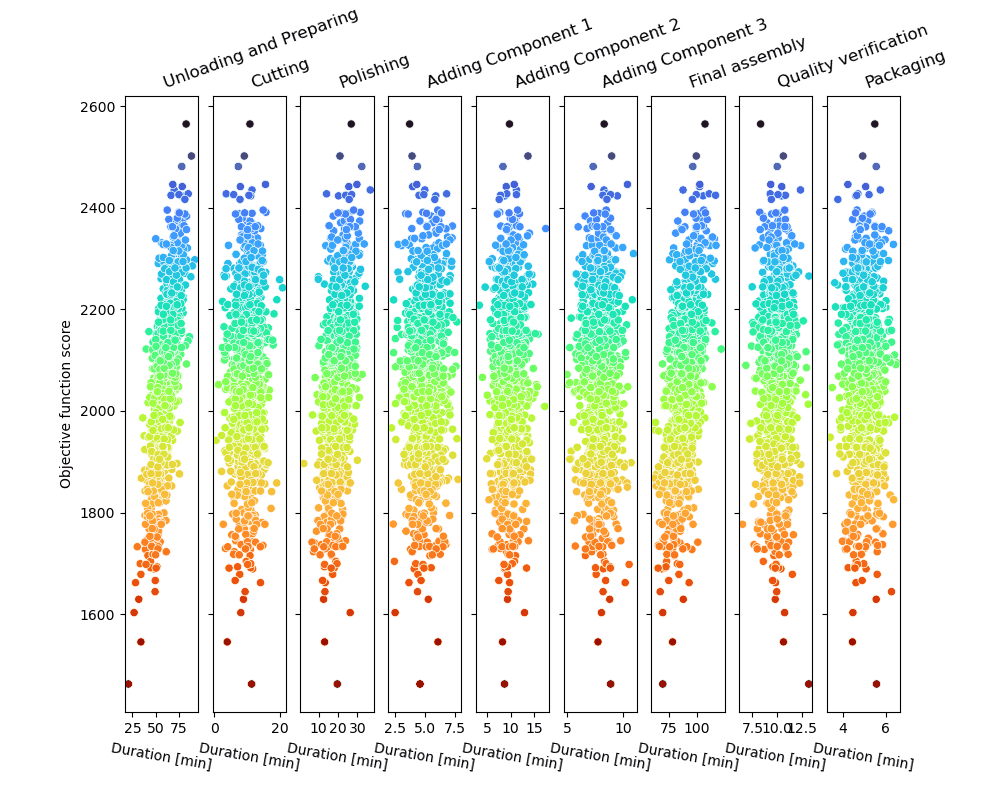
La boucle d’échantillonnage Monte-Carlo produira une série de trajectoires de processus possibles et les notera, comme illustré dans la figure. Monte Carlo trajectories for different process scenario.

Cet exercice fait partie du cours

Simulation d’événements discrets en Python

Afficher le cours

Instructions

Ajoutez la contribution au score de chaque processus, sachant que la durée des processus est stockée dans process_duration_all[s, p] et leur poids respectif dans proc_p["score_weight_0_10"].
Paramétrez la boucle for pour exécuter NUM_SIMULATIONS itérations Monte-Carlo avec s comme variable muette.
Lancez le moteur Monte Carlo stocké dans la fonction run_monte_carlo() (cela génèrera les graphiques « score » et « rank »)

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

def objective_function_calc():
    objective_func = np.ones(NUM_SIMULATIONS)

    for s in range(NUM_SIMULATIONS):
        for p in range(len(processes)):
            proc_p = processes[p]
            
            # Add the score contribution of each process
            objective_func[s] += ____

    plot_results(objective_func)

def run_monte_carlo():

    # Set the for-loop to run NUM_SIMULATIONS Monte-Carlo runs 
    ____

        env = simpy.Environment()
        env.process(manufractoring_process(env, s))
        env.run()

    objective_function_calc()

# Run the Monte Carlo function
____

Modifier et exécuter le code