Échantillonnage Monte-Carlo pour les modèles à événements discrets

Imaginez une usine qui fabrique des horloges murales. Leur popularité augmente et la demande dépasse désormais la capacité de production. L’usine tourne à plein régime depuis des mois, et vous souhaitez mieux comprendre son fonctionnement et ses goulets d’étranglement afin de prendre des décisions de gestion plus éclairées et de planifier les investissements et l’extension à venir.

Un modèle à événements discrets des processus de l’usine a été développé, et vous souhaitez maintenant exécuter une analyse par échantillonnage Monte-Carlo pour explorer différents scénarios. Le processus de fabrication est résumé dans le tableau ci-dessous, et les informations ont été stockées dans une liste de dictionnaires nommée processes, avec un dictionnaire par processus. Les clés de ces dictionnaires correspondent aux en-têtes des colonnes du tableau. Les paquets suivants ont été importés pour vous : numpy as np, matplotlib.pyplot as plt, seaborn as sns, random, pandas as pd et time.

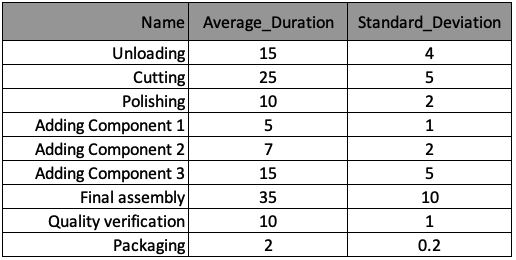
Table with process names and their duration statistics, namely mean and standard deviation.

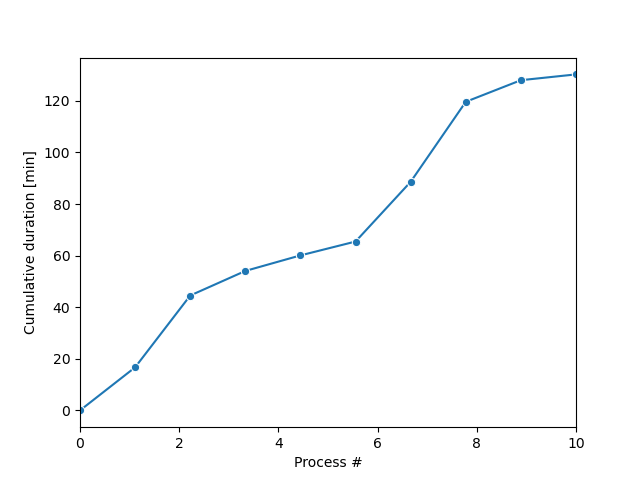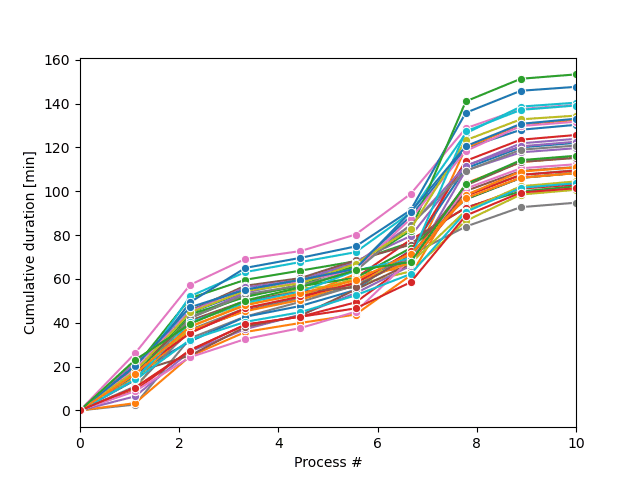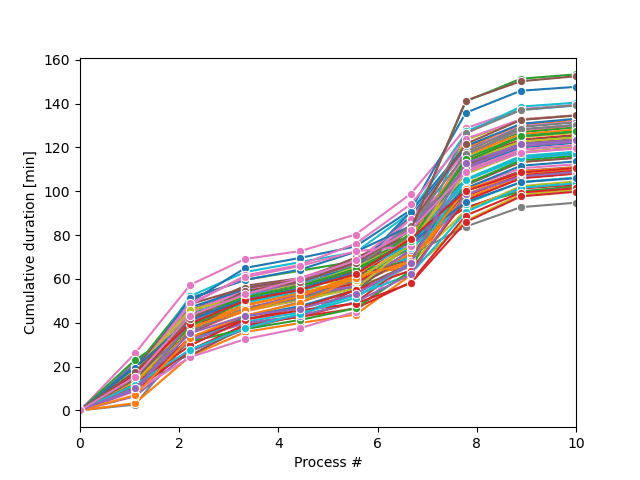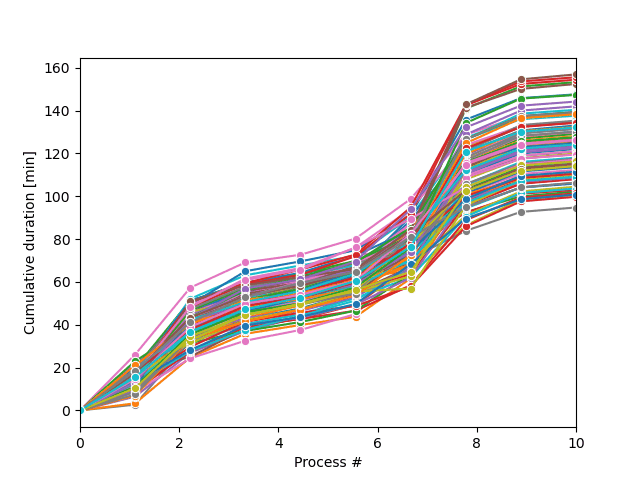
La boucle d’échantillonnage Monte-Carlo produira une série de trajectoires possibles des processus, comme illustré sur la figure. Monte Carlo trajectories for different process scenario.

Cet exercice fait partie du cours

Simulation d’événements discrets en Python

Afficher le cours

Instructions

Mettez en place la boucle principale for d’échantillonnage Monte-Carlo pour n_trajectories échantillons avec la variable factice t.
Utilisez la distribution gaussienne du paquet random pour estimer de manière pseudo-aléatoire la durée des processus.

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

n_trajectories = 100

# Run a Monte-Carlo for-loop for n_trajectories samples
____

    for p in range(len(processes)):
        proc_p = processes[p]

        # Random gauss method to pseudo-randomly estimate process duration
        process_duration = ____(proc_p["Average_Duration"], proc_p["Standard_Deviation"])
        time_record[p + 1] = time_record[p] + process_duration

    df_disc = pd.DataFrame({cNam[0]: process_line_space, cNam[1]: time_record})
    fig = sns.lineplot(data=df_disc, x=cNam[0], y=cNam[1], marker="o")  # Step_10
    fig.set(xlim=(0, len(processes) + 1))
    plt.plot()
plt.grid()
plt.show()

Modifier et exécuter le code