Production de vêtements : multiprocessus et modularité
On vous a demandé de créer un modèle à événements discrets pour optimiser une usine de confection située à Milan, capitale de la mode.
Vous êtes très enthousiaste et vous voulez bâtir un modèle utile et évolutif, car vous savez que l’industrie de l’habillement est complexe et fait intervenir de nombreux processus et ressources, avec lesquels vous vous familiarisez encore.
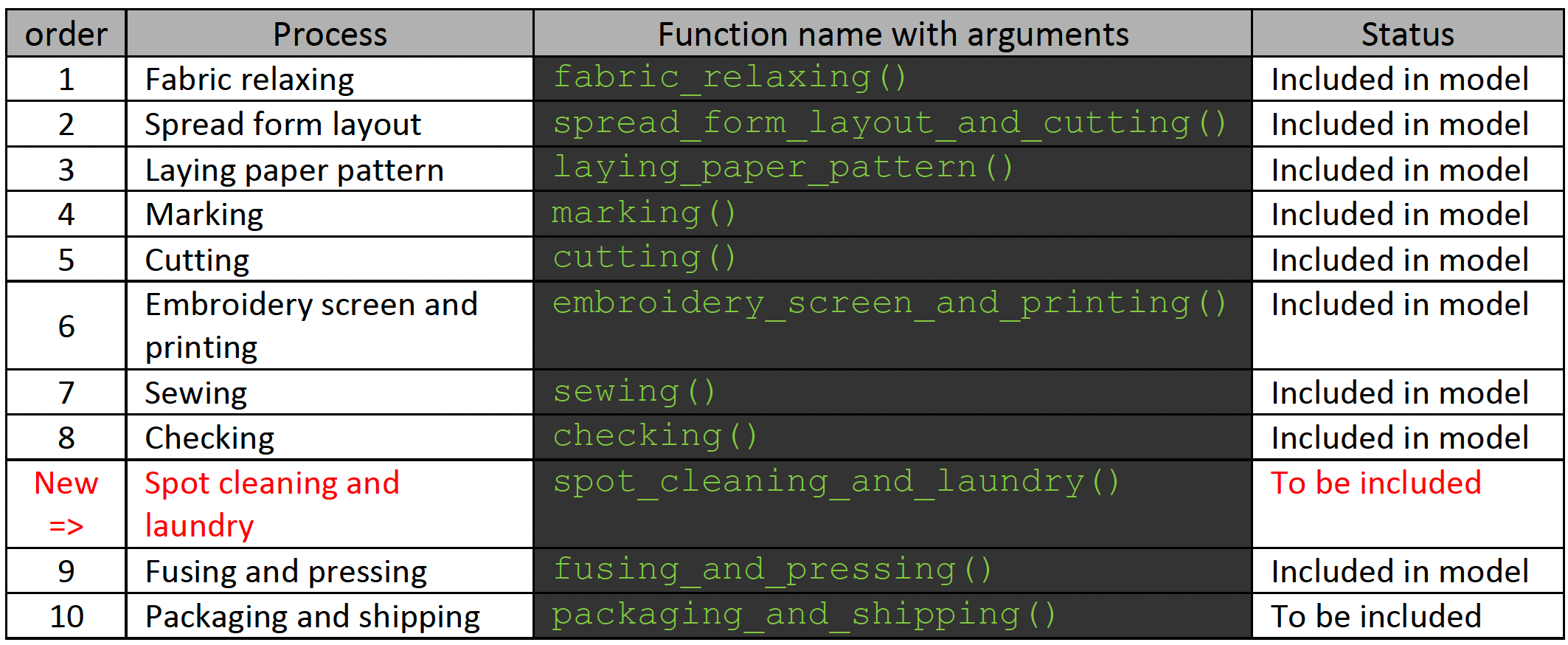
Vous avez mené vos recherches et établi la liste des processus présentés dans le tableau ci-dessous. Vous avez été rigoureux et créé une fonction séparée pour chaque processus afin de rendre votre modèle modulaire et de lui permettre d’évoluer de manière maîtrisée.
Vous avez maintenant reçu un retour de votre responsable : il faut intégrer un nouveau processus dans le modèle pour prendre en compte « Spot cleaning and laundry », qui doit se situer entre les étapes 8 et 9 (voir la ligne du tableau en rouge). Les packages random et simpy ont été importés.
Cet exercice fait partie du cours
Simulation d’événements discrets en Python
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Create a function for the new process
def ____(gen_type=None, gauss_mean=None, gauss_std=None, unif_start=None, unif_end=None):
if gen_type == "gauss":
duration = random.gauss(gauss_mean, gauss_std)
elif gen_type == "uniform":
duration = random.uniform(unif_start, unif_end)
return duration
def all_processes(env, prod_line):
with prod_line.request() as request:
yield request
t1 = fabric_relaxing(gen_type="gauss", gauss_mean=2*60, gauss_std=15)
t2 = spread_form_layout(gen_type="gauss", gauss_mean=6, gauss_std=1)
t3 = laying_paper_pattern(gen_type="uniform", unif_start=3, unif_end=0.5)
t4 = marking(gen_type="gauss", gauss_mean=6, gauss_std=1)
t5 = cutting(gen_type="gauss", gauss_mean=5, gauss_std=0.5)
t6 = embroidery_screen_and_printing(gen_type="uniform", unif_start=10, unif_end=2)
t7 = sewing(gen_type="gauss", gauss_mean=15, gauss_std=3)
t8 = checking(gen_type="gauss", gauss_mean=2, gauss_std=0.5)
# Add the new process
tnew = ____
# Account for the new process duration in the entire process duration
total_duration = sum([t1, t2, t3, t4, t5, t6, t7, t8, ____, t9, t10])
yield env.timeout(total_duration)