Optimisation de la production : Search & Stop
Utilisons le modèle d’usine d’horloges murales créé dans un exercice précédent et déployons une approche d’optimisation « Search & Stop » basée sur un échantillonnage Monte-Carlo pour identifier les goulets d’étranglement critiques.
Le processus de fabrication est résumé dans le tableau ci-dessous, et les informations ont été stockées dans une liste de dictionnaires nommée processes, avec un dictionnaire par processus. Les clés de chaque dictionnaire correspondent aux en-têtes de colonnes du tableau.
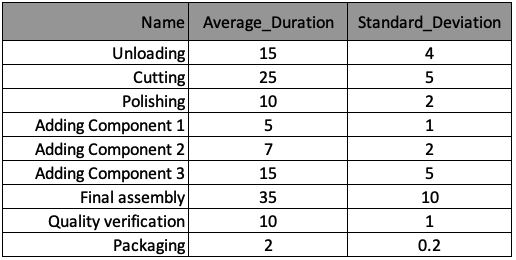
La méthode plot_results() pour générer les graphiques de cet exercice a été préchargée et est présentée ci-dessous.
def plot_results():
df_disc = pd.DataFrame({cNam[0]: process_line_space, cNam[1]: time_record})
fig = sns.lineplot(data=df_disc, x=cNam[0], y=cNam[1], marker='o')
plt.grid()
fig.set(xlim=(0, len(processes)))
fig.set(ylim=(0, 180))
fig.set(xticks=process_line_space)
plt.plot()
La boucle d’échantillonnage Monte-Carlo produira une série de trajectoires de processus possibles et s’arrêtera lorsque la condition souhaitée sera satisfaite, comme illustré sur la figure.
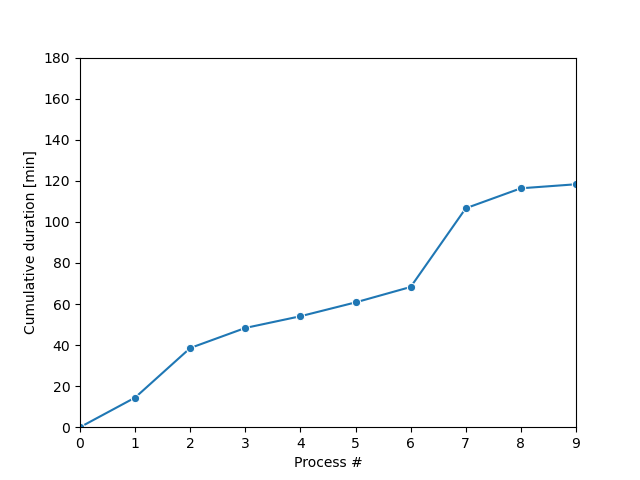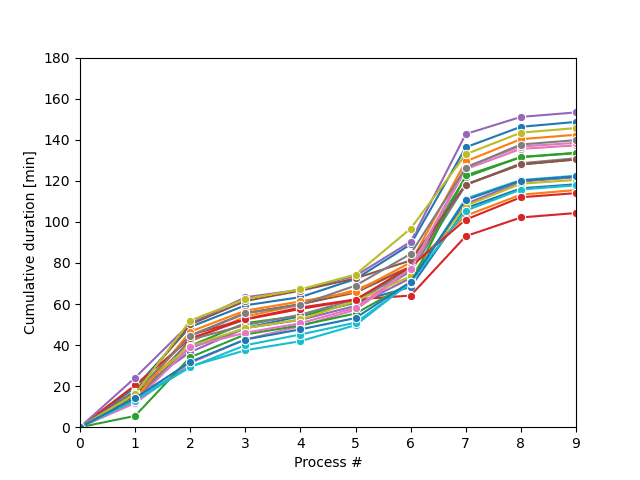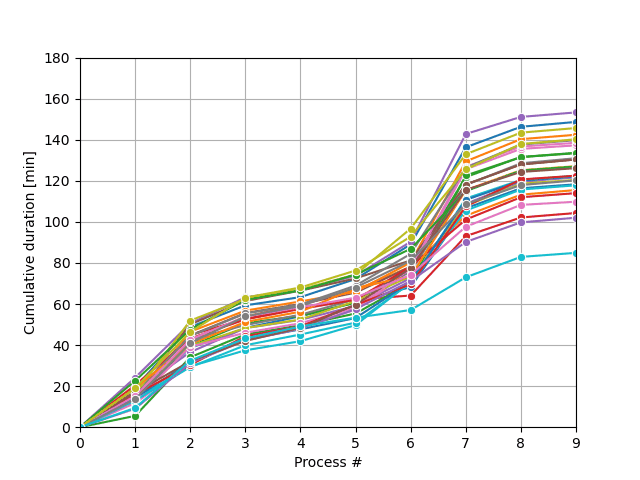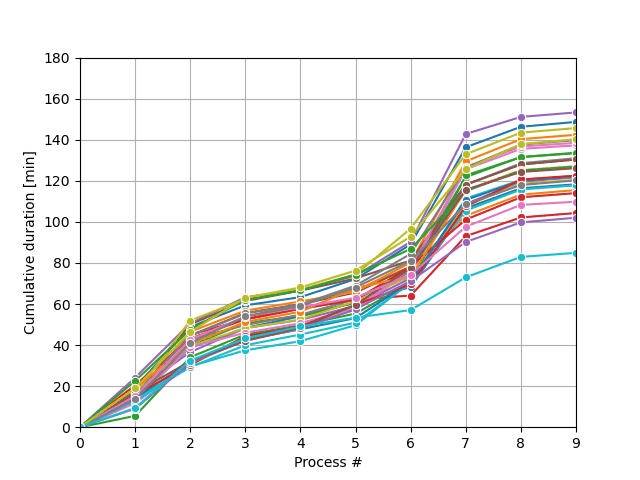
Cet exercice fait partie du cours
Simulation d’événements discrets en Python
Instructions
- Créez une boucle pour exécuter des trajectoires de simulation tant que
run_iest égal à zéro ou quetotal_duration[run_i]est supérieur à 85 heures (c.-à-d. condition d’arrêt :total_duration[run_i]inférieure ou égale à 85 heures). - Exécutez le moteur Monte Carlo stocké dans la fonction
run_monte_carlo().
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
def run_monte_carlo():
run_i = 0
# While-loop with the stop condition
____
run_i += 1
env = simpy.Environment()
env.process(manufractoring_process(env))
env.run()
plot_results()
plt.show()
# Call the run_monte_carlo function
____