Falsche deterministische Berechnung

In dieser und der nächsten Übung spielst du mit den pi-Berechnungen aus dem Video, um die Bedeutung jedes Schritts im Simulationsprozess besser zu verstehen.

Erinnere dich: Die Simulation zur Bestimmung von pi erzeugt zufällige Punkte \((x, y)\), wobei \(x\) und \(y\) zwischen −1 und 1 liegen, wie im Diagramm unten gezeigt.

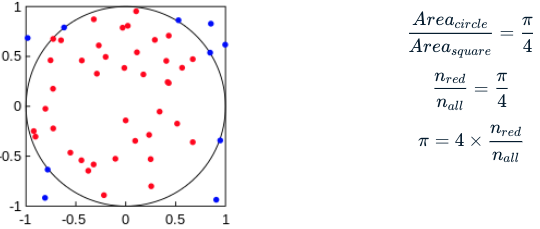
A graph of a circle inside a square with randomly sampled points

Was wäre, wenn du die deterministische Berechnung, mit der du prüfst, ob ein Punkt zu circle_points hinzugefügt werden soll, fälschlicherweise änderst? Wie wirkt sich das auf das Endergebnis aus? An dem schrägen Wert, den du für pi erhältst, wirst du sehen: Die korrekte Angabe deterministischer Berechnungen ist für Monte-Carlo-Simulationen entscheidend!

random wurde bereits für dich importiert.

Diese Übung ist Teil des Kurses

Monte-Carlo-Simulationen in Python

Kurs anzeigen

Anleitung zur Übung

Erhöhe circle_points für jeden Punkt, dessen Abstand vom Ursprung kleiner als 0,75 ist (statt eines Abstands von eins, wie im Video gezeigt).

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

n = 10000
circle_points = 0 
square_points = 0 
for i in range(n):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    dist_from_origin = x**2 + y**2
    # Increment circle_points for any point with a distance from origin of less than .75
    if ____:
        circle_points += 1
    square_points += 1
pi = 4 * circle_points / square_points
print(pi)

Code bearbeiten und ausführen