Taille d’effet pour des moyennes
De nombreuses entreprises financées par du capital‑risque reçoivent plus d’un tour de financement. En général, le deuxième tour est plus important que le premier. Dans quelle mesure le numéro du tour influe‑t‑il sur le montant moyen levé ? Vous pouvez quantifier cela avec le d de Cohen.
Rappelez‑vous que, pour calculer le d de Cohen, vous devez d’abord calculer l’écart type regroupé (pooled). Il est donné par la formule
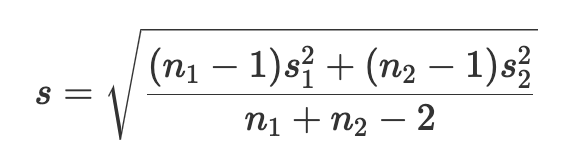
Le d de Cohen est ensuite donné par :

Un DataFrame d’investissements en capital‑risque (investments_df) a été chargé pour vous, ainsi que les packages pandas sous pd, NumPy sous np et stats de SciPy. La colonne funding_total_usd indique le montant total levé lors de ce tour.
Cet exercice fait partie du cours
Fondements de l’inférence en Python
Instructions
- Filtrez
investments_dfpour sélectionner séparément lesfunding_rounds1 et 2. - Calculez l’écart type et la taille d’échantillon pour chaque tour.
- Calculez l’écart type regroupé entre les deux tours.
- Calculez le d de Cohen à partir des éléments que vous venez de déterminer.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Select all investments from rounds 1 and 2 separately
round1_df = investments_df[____['funding_rounds'] == ____]
round2_df = investments_df[____['funding_rounds'] == ____]
# Calculate the standard deviation of each round and the number of companies in each round
round1_sd = ____.std()
round2_sd = ____.std()
round1_n = ____.shape[0]
round2_n = ____.shape[0]
# Calculate the pooled standard deviation between the two rounds
pooled_sd = np.sqrt(((____ - 1) * ____ ** 2 + (____ - 1) *____ ** 2) / (____ + ____ - 2))
# Calculate Cohen's d
d = (____.mean() - ____.mean()) / ____