Utilisation du parcours de pré-ordre avec la notation polonaise
Les arbres d'expression sont une sorte d'arbre binaire qui représente des expressions arithmétiques :
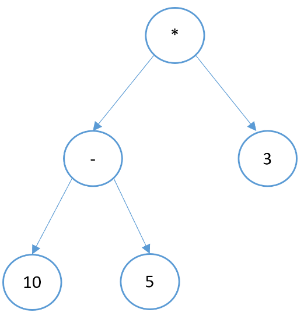
En appliquant un parcours dans l'ordre à un arbre d'expression, vous pouvez obtenir la notation infixe. Cette notation pour l'arbre donné sera (10-5)*3.
En appliquant un parcours de préordre à un arbre d'expression, vous pouvez obtenir la notation préfixe, également appelée notation polonaise, dans laquelle l'opérateur apparaît avant ses opérandes. Cette notation pour l'arbre donné sera *-10 5 3.
En appliquant un parcours post-ordre à un arbre d'expression, vous pouvez obtenir la notation postfixe, également appelée notation polonaise inversée, dans laquelle l'opérateur apparaît après ses opérandes. Cette notation pour l'arbre donné sera 10 5- 3*.
Codez le parcours de pré-ordre de façon à obtenir la notation du préfixe de cet arbre d'expression.
Cet exercice fait partie du cours
Structures de données et algorithmes en Python
Instructions
- Vérifiez si
current_nodeexiste. - Imprimez la valeur de l'adresse
current_node. - Appelez la fonction
pre_order()de manière récursive sur les moitiés appropriées de l'arbre.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
import queue
class ExpressionTree:
def __init__(self):
self.root = None
def pre_order(self, current_node):
# Check if current_node exists
____:
# Print the value of the current_node
____
# Call pre_order recursively on the appropriate half of the tree
____
____
et = CreateExpressionTree()
et.pre_order(et.root)