Lokale Minima vermeiden
In der vorherigen Aufgabe hast du gesehen, wie leicht man in lokalen Minima stecken bleiben kann. Wir hatten ein einfaches Optimierungsproblem mit einer Variable, und dennoch hat der Gradientenabstieg das globale Minimum nicht gefunden, weil er zuerst durch lokale Minima musste. Eine Möglichkeit, dieses Problem zu umgehen, ist die Verwendung von Momentum. Dadurch kann der Optimierer lokale Minima „durchbrechen“. Wir verwenden wieder die Verlustfunktion aus der vorherigen Aufgabe, die als loss_function() definiert ist und für dich bereitsteht.
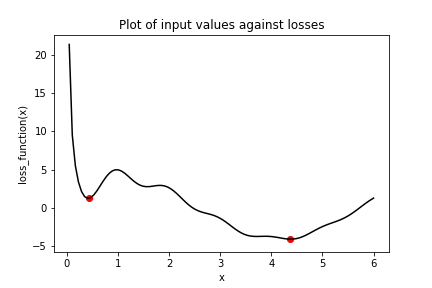
Mehrere Optimierer in tensorflow haben einen Momentum-Parameter, darunter SGD und RMSprop. In dieser Übung verwendest du RMSprop. Beachte, dass x_1 und x_2 diesmal auf denselben Wert initialisiert wurden. Außerdem wurde keras.optimizers.RMSprop() bereits aus tensorflow für dich importiert.
Diese Übung ist Teil des Kurses
Einführung in TensorFlow mit Python
Anleitung zur Übung
- Setze die Operation
opt_1auf eine Lernrate von 0,01 und ein Momentum von 0,99. - Setze
opt_2auf den Root-Mean-Square-Propagation-(RMS)-Optimierer mit einer Lernrate von 0,01 und einem Momentum von 0,00. - Definiere die Minimierungsoperation für
opt_2. - Gib
x_1undx_2alsnumpy-Arrays aus.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Initialize x_1 and x_2
x_1 = Variable(0.05,float32)
x_2 = Variable(0.05,float32)
# Define the optimization operation for opt_1 and opt_2
opt_1 = keras.optimizers.RMSprop(learning_rate=____, momentum=____)
opt_2 = ____
for j in range(100):
opt_1.minimize(lambda: loss_function(x_1), var_list=[x_1])
# Define the minimization operation for opt_2
____
# Print x_1 and x_2 as numpy arrays
print(____, ____)