Optimizing with gradients

You are given a loss function, \(y = x^{2}\), which you want to minimize. You can do this by computing the slope using the GradientTape() operation at different values of x. If the slope is positive, you can decrease the loss by lowering x. If it is negative, you can decrease it by increasing x. This is how gradient descent works.

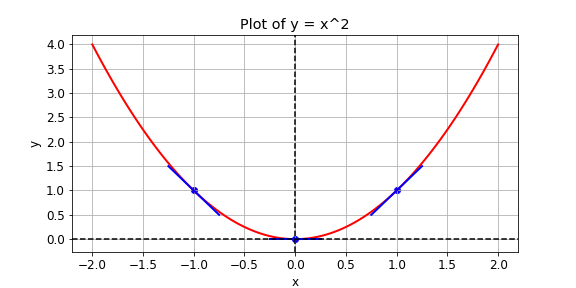
The image shows a plot of y equals x squared. It also shows the gradient at x equals -1, x equals 0, and x equals 1.

In practice, you will use a high level tensorflow operation to perform gradient descent automatically. In this exercise, however, you will compute the slope at x values of -1, 1, and 0. The following operations are available: GradientTape(), multiply(), and Variable().

Diese Übung ist Teil des Kurses

Introduction to TensorFlow in Python

Anleitung zur Übung

Define x as a variable with the initial value x0.
Set the loss function, y, equal to x multiplied by x. Do not make use of operator overloading.
Set the function to return the gradient of y with respect to x.

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

def compute_gradient(x0):
  	# Define x as a variable with an initial value of x0
	x = ____(x0)
	with GradientTape() as tape:
		tape.watch(x)
        # Define y using the multiply operation
		y = ____
    # Return the gradient of y with respect to x
	return tape.gradient(____, ____).numpy()

# Compute and print gradients at x = -1, 1, and 0
print(compute_gradient(-1.0))
print(compute_gradient(1.0))
print(compute_gradient(0.0))

Code bearbeiten und ausführen

Diese Übung ist Teil des Kurses

Introduction to TensorFlow in Python

Mittlere SchwierigkeitSchwierigkeitsgrad

4.9+

Kurs kostenlos starten

Before you can build advanced models in TensorFlow 2, you will first need to understand the basics. In this chapter, you’ll learn how to define constants and variables, perform tensor addition and multiplication, and compute derivatives. Knowledge of linear algebra will be helpful, but not necessary.

Exercise 1: Constants and variables Exercise 2: Defining data as constants Exercise 3: Defining variables Exercise 4: Basic operations Exercise 5: Performing element-wise multiplication Exercise 6: Making predictions with matrix multiplication Exercise 7: Summing over tensor dimensions Exercise 8: Advanced operations Exercise 9: Reshaping tensors Exercise 10: Optimizing with gradients

Aktuelle Übung

Exercise 11: Working with image data

In this chapter, you will learn how to build, solve, and make predictions with models in TensorFlow 2. You will focus on a simple class of models – the linear regression model – and will try to predict housing prices. By the end of the chapter, you will know how to load and manipulate data, construct loss functions, perform minimization, make predictions, and reduce resource use with batch training.

Exercise 1: Input data Exercise 2: Load data using pandas Exercise 3: Setting the data type Exercise 4: Loss functions Exercise 5: Loss functions in TensorFlow Exercise 6: Modifying the loss function Exercise 7: Linear regression Exercise 8: Set up a linear regression Exercise 9: Train a linear model Exercise 10: Multiple linear regression Exercise 11: Batch training Exercise 12: Preparing to batch train Exercise 13: Training a linear model in batches

The previous chapters taught you how to build models in TensorFlow 2. In this chapter, you will apply those same tools to build, train, and make predictions with neural networks. You will learn how to define dense layers, apply activation functions, select an optimizer, and apply regularization to reduce overfitting. You will take advantage of TensorFlow's flexibility by using both low-level linear algebra and high-level Keras API operations to define and train models.

Exercise 1: Dense layers Exercise 2: The linear algebra of dense layers Exercise 3: The low-level approach with multiple examples Exercise 4: Using the dense layer operation Exercise 5: Activation functions Exercise 6: Binary classification problems Exercise 7: Multiclass classification problems Exercise 8: Optimizers Exercise 9: The dangers of local minima Exercise 10: Avoiding local minima Exercise 11: Training a network in TensorFlow Exercise 12: Initialization in TensorFlow Exercise 13: Defining the model and loss function Exercise 14: Training neural networks with TensorFlow

In the final chapter, you'll use high-level APIs in TensorFlow 2 to train a sign language letter classifier. You will use both the sequential and functional Keras APIs to train, validate, make predictions with, and evaluate models. You will also learn how to use the Estimators API to streamline the model definition and training process, and to avoid errors.

Exercise 1: Defining neural networks with Keras Exercise 2: The sequential model in Keras Exercise 3: Compiling a sequential model Exercise 4: Defining a multiple input model Exercise 5: Training and validation with Keras Exercise 6: Training with Keras Exercise 7: Metrics and validation with Keras Exercise 8: Overfitting detection Exercise 9: Evaluating models Exercise 10: Training models with the Estimators API Exercise 11: Preparing to train with Estimators Exercise 12: Defining Estimators Exercise 13: Congratulations!