Fertigungsoptimierung: Score & Rank

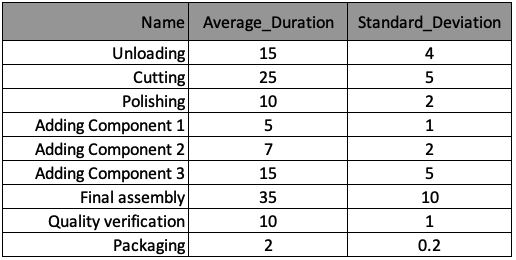
Lass uns dasselbe ereignisdiskrete Modell der Wanduhrfabrik verwenden und eine "Score & Rank"-Optimierungsroutine aufsetzen. Zur Erinnerung ist der Fertigungsprozess in der folgenden Tabelle nochmals zusammengefasst. Die Informationen wurden in einer Liste von Dictionaries namens processes gespeichert, mit einem Dictionary pro Prozess. Die Schlüssel in diesen Dictionaries entsprechen den Spaltenüberschriften der Tabelle.

Table with process names and their duration statistics, namely mean and standard deviation.

Die Methode plot_results(), die in dieser Übung für die Diagramme verwendet wird, wurde vorab geladen und ist unten dargestellt.

def plot_results(objective_func):
    # Score
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.scatterplot(ax=axes[p], x=process_duration_all[:, p], y=objective_func, c=objective_func, cmap="turbo_r")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Duration [min]", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Objective function score")
    plt.show()

    # Rank
    index_sort = np.argsort(objective_func)
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.lineplot(ax=axes[p], x=np.linspace(0, NUM_SIMULATIONS, NUM_SIMULATIONS),
                     y=process_duration_all[index_sort, p], color="orchid")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Score-ranked scenarios", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Duration [min]")
    plt.show()

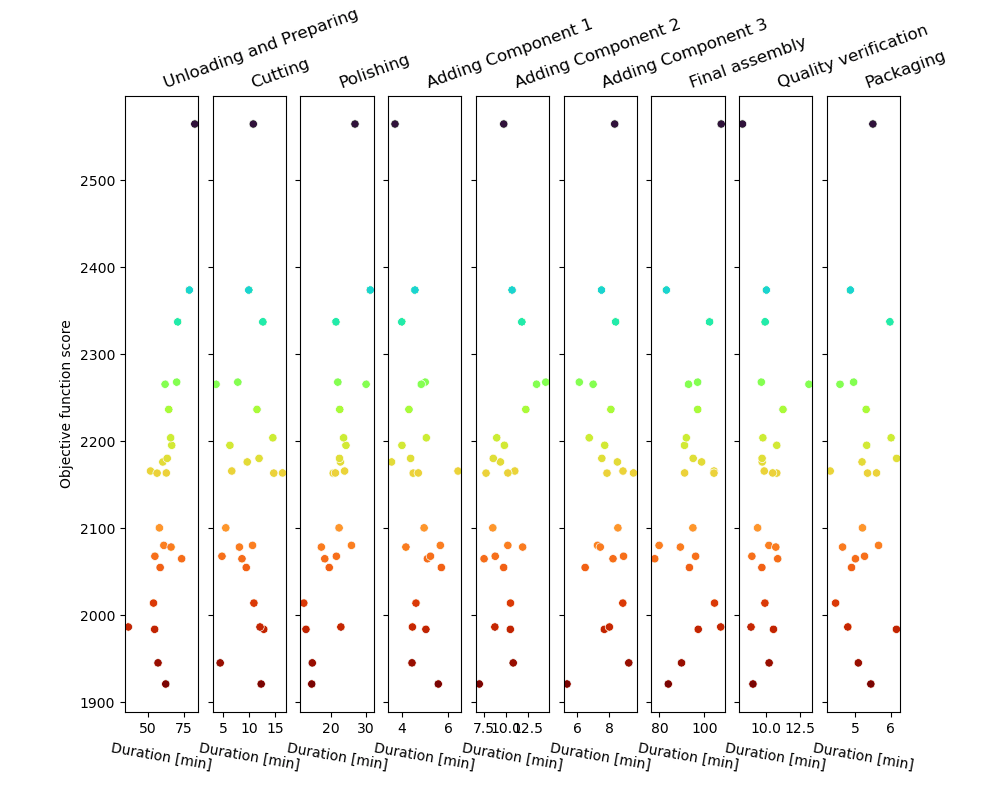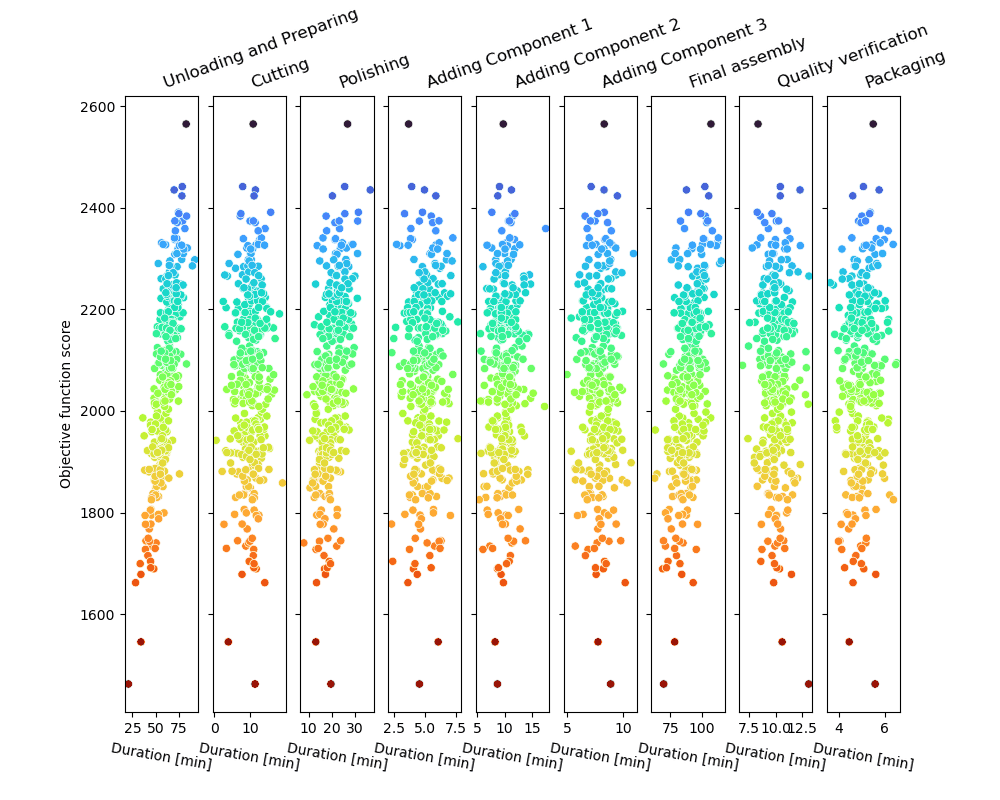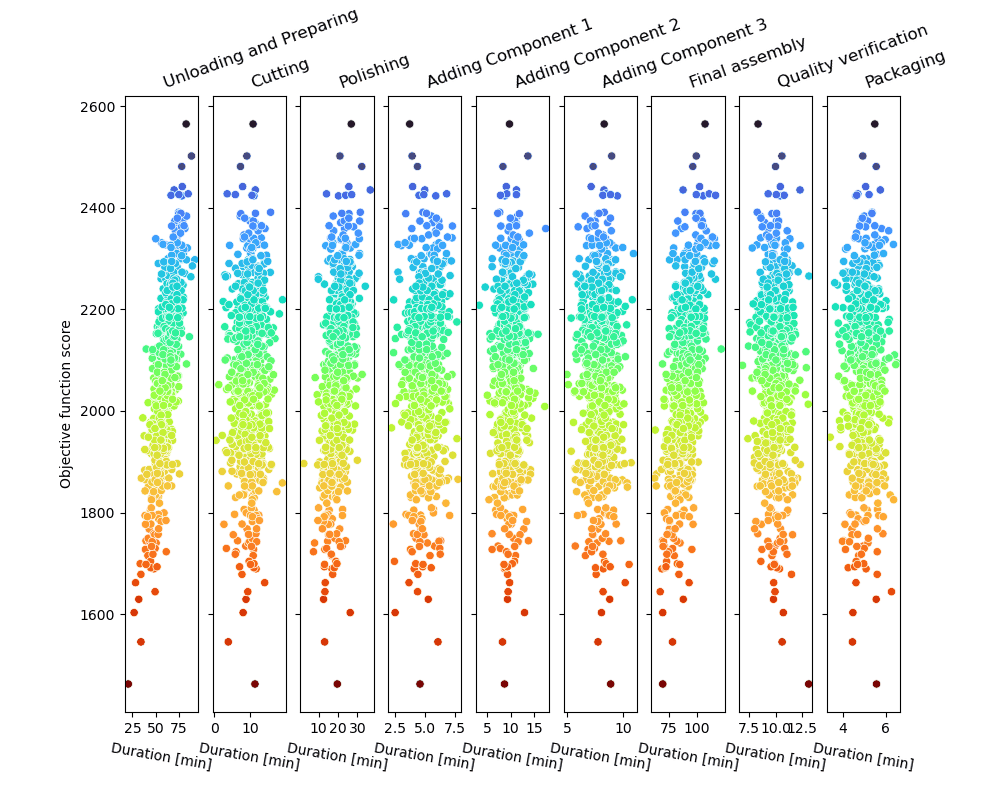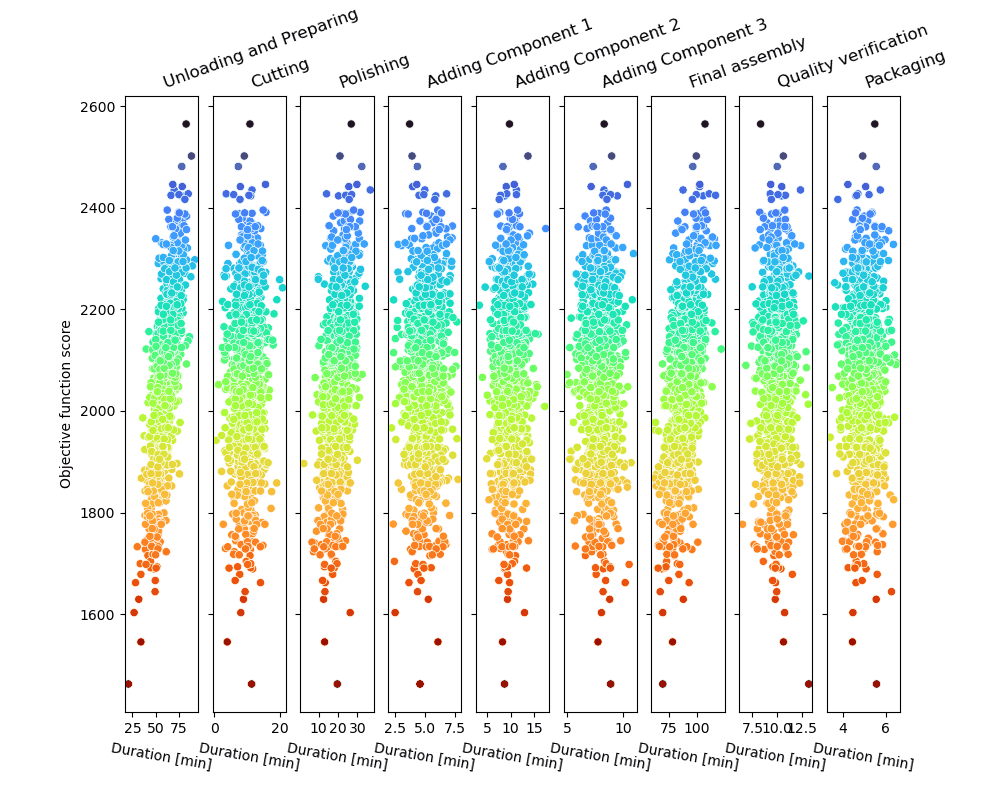
Die Monte-Carlo-Sampling-Schleife erzeugt eine Reihe möglicher Prozessverläufe und bewertet sie – wie in der Abbildung gezeigt. Monte Carlo trajectories for different process scenario.

Diese Übung ist Teil des Kurses

Diskrete-Ereignis-Simulation mit Python

Kurs anzeigen

Anleitung zur Übung

Addiere den Score-Beitrag jedes Prozesses. Die Prozessdauern findest du in process_duration_all[s, p], die jeweiligen Gewichte in proc_p["score_weight_0_10"].
Setze die for-Schleife so auf, dass NUM_SIMULATIONS Monte-Carlo-Läufe mit s als Laufvariable ausgeführt werden.
Starte die Monte-Carlo-Engine über die Funktion run_monte_carlo() (dies erzeugt sowohl die "score"- als auch die "rank"-Diagramme).

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

def objective_function_calc():
    objective_func = np.ones(NUM_SIMULATIONS)

    for s in range(NUM_SIMULATIONS):
        for p in range(len(processes)):
            proc_p = processes[p]
            
            # Add the score contribution of each process
            objective_func[s] += ____

    plot_results(objective_func)

def run_monte_carlo():

    # Set the for-loop to run NUM_SIMULATIONS Monte-Carlo runs 
    ____

        env = simpy.Environment()
        env.process(manufractoring_process(env, s))
        env.run()

    objective_function_calc()

# Run the Monte Carlo function
____

Code bearbeiten und ausführen