Bekleidungsproduktion: Mehrere Prozesse und Modularität
Du wurdest gebeten, ein ereignisdiskretes Modell zu erstellen, um eine Bekleidungsfabrik in Mailand, der Modehauptstadt Italiens, zu optimieren.
Du bist supermotiviert und möchtest sicherstellen, dass du ein hilfreiches und skalierbares Modell baust, denn du weißt: Die Bekleidungsindustrie ist komplex und umfasst viele Prozesse und Ressourcen, mit denen du dich noch vertraut machst.
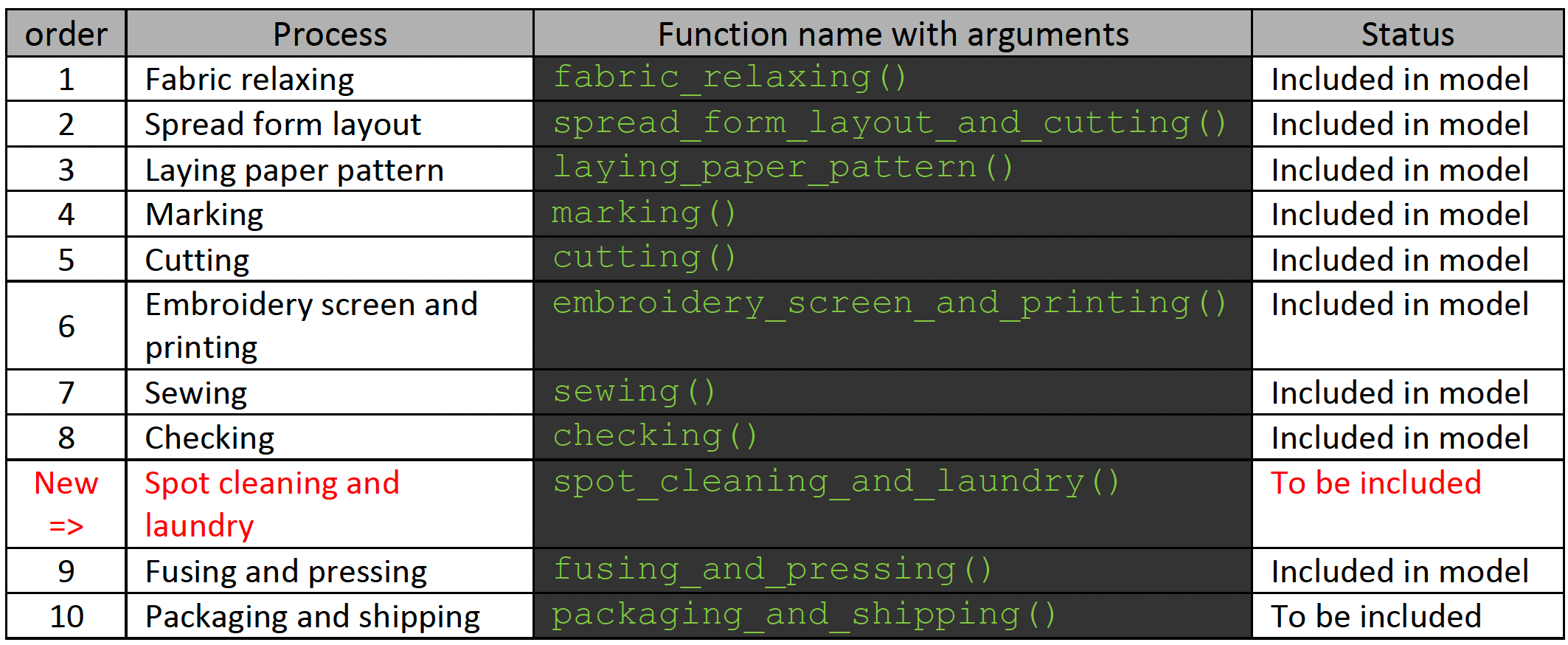
Du hast recherchiert und die untenstehende Liste von Prozessen zusammengestellt. Du warst sorgfältig und hast für jeden Prozess eine eigene Funktion erstellt, um dein Modell modular zu halten und ein kontrolliertes Wachstum zu ermöglichen.
Jetzt hast du Feedback von deiner Führungskraft erhalten: Du sollst einen neuen Prozess in das Modell aufnehmen, und zwar „Spot cleaning and laundry“. Dieser soll zwischen Schritt 8 und 9 liegen (siehe die rot markierte Tabellenzeile). Die Pakete random und simpy wurden importiert.
Diese Übung ist Teil des Kurses
Diskrete-Ereignis-Simulation mit Python
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Create a function for the new process
def ____(gen_type=None, gauss_mean=None, gauss_std=None, unif_start=None, unif_end=None):
if gen_type == "gauss":
duration = random.gauss(gauss_mean, gauss_std)
elif gen_type == "uniform":
duration = random.uniform(unif_start, unif_end)
return duration
def all_processes(env, prod_line):
with prod_line.request() as request:
yield request
t1 = fabric_relaxing(gen_type="gauss", gauss_mean=2*60, gauss_std=15)
t2 = spread_form_layout(gen_type="gauss", gauss_mean=6, gauss_std=1)
t3 = laying_paper_pattern(gen_type="uniform", unif_start=3, unif_end=0.5)
t4 = marking(gen_type="gauss", gauss_mean=6, gauss_std=1)
t5 = cutting(gen_type="gauss", gauss_mean=5, gauss_std=0.5)
t6 = embroidery_screen_and_printing(gen_type="uniform", unif_start=10, unif_end=2)
t7 = sewing(gen_type="gauss", gauss_mean=15, gauss_std=3)
t8 = checking(gen_type="gauss", gauss_mean=2, gauss_std=0.5)
# Add the new process
tnew = ____
# Account for the new process duration in the entire process duration
total_duration = sum([t1, t2, t3, t4, t5, t6, t7, t8, ____, t9, t10])
yield env.timeout(total_duration)