Monte-Carlo-Sampling für ereignisdiskrete Modelle

Stell dir eine Fabrik vor, die Wanduhr en produziert. Die Uhren werden immer beliebter, und die Nachfrage ist inzwischen höher als die Produktionskapazität. Die Fabrik läuft seit Monaten unter Volllast, und du möchtest ihr Verhalten und ihre Engpässe besser verstehen, um fundiertere Managemententscheidungen treffen und zukünftige Investitionen sowie Erweiterungen planen zu können.

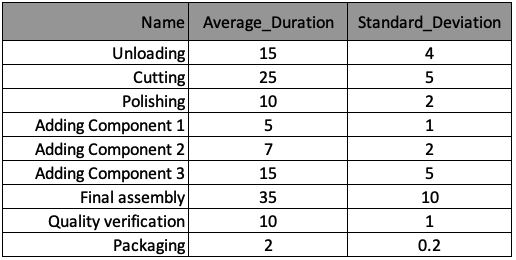
Ein ereignisdiskretes Modell der Fabrikprozesse wurde entwickelt, und nun möchtest du eine Monte-Carlo-Sampling-Analyse durchführen, um Szenarien zu erkunden. Der Fertigungsprozess ist in der untenstehenden Tabelle zusammengefasst; die Informationen wurden in einer Liste von Dictionaries namens processes gespeichert, mit einem Dictionary pro Prozess. Die Keys dieser Dictionaries entsprechen den Spaltenüberschriften der Tabelle. Folgende Pakete wurden bereits importiert: numpy as np, matplotlib.pyplot as plt, seaborn as sns, random, pandas as pd und time.

Table with process names and their duration statistics, namely mean and standard deviation.

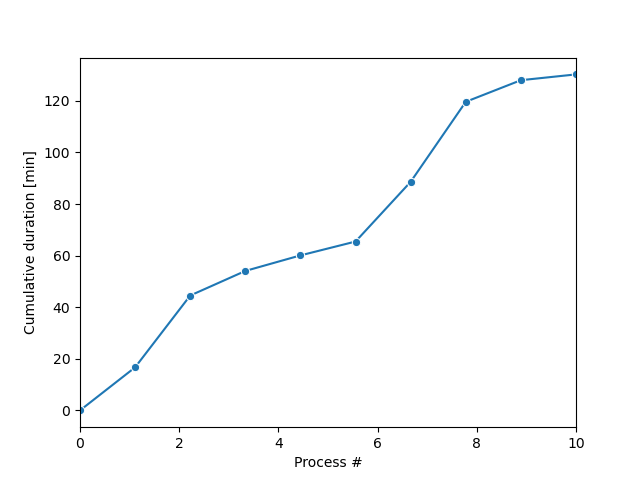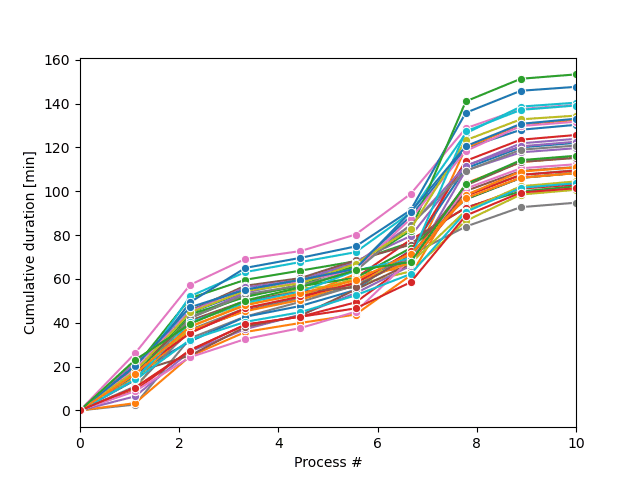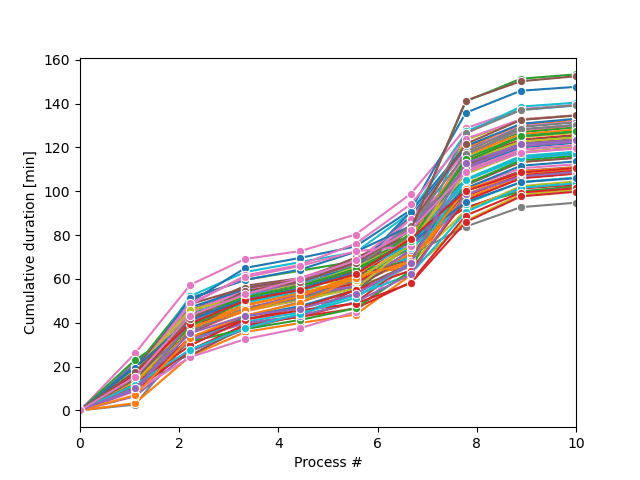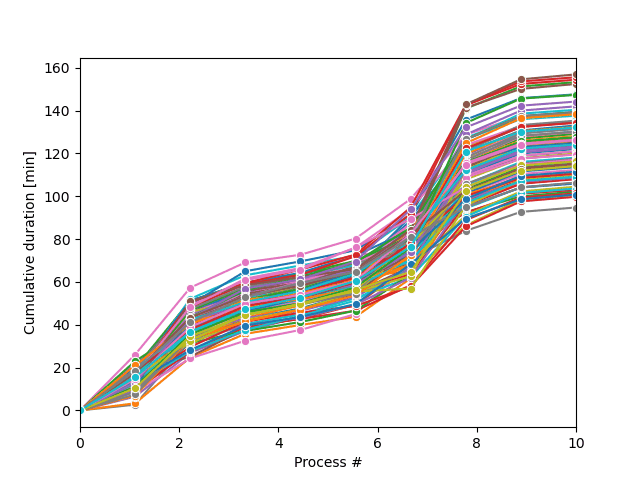
Die Monte-Carlo-Sampling-Schleife erzeugt eine Reihe möglicher Prozesstrajektorien, wie in der Abbildung gezeigt. Monte Carlo trajectories for different process scenario.

Diese Übung ist Teil des Kurses

Diskrete-Ereignis-Simulation mit Python

Kurs anzeigen

Anleitung zur Übung

Richte die äußere Monte-Carlo-Sampling-for-Schleife für n_trajectories Stichproben mit der Dummy-Variablen t ein.
Verwende die Gauß-Verteilung aus dem Paket random, um die Prozessdauer pseudozufällig zu schätzen.

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

n_trajectories = 100

# Run a Monte-Carlo for-loop for n_trajectories samples
____

    for p in range(len(processes)):
        proc_p = processes[p]

        # Random gauss method to pseudo-randomly estimate process duration
        process_duration = ____(proc_p["Average_Duration"], proc_p["Standard_Deviation"])
        time_record[p + 1] = time_record[p] + process_duration

    df_disc = pd.DataFrame({cNam[0]: process_line_space, cNam[1]: time_record})
    fig = sns.lineplot(data=df_disc, x=cNam[0], y=cNam[1], marker="o")  # Step_10
    fig.set(xlim=(0, len(processes) + 1))
    plt.plot()
plt.grid()
plt.show()

Code bearbeiten und ausführen