Entropien der Kindknoten berechnen
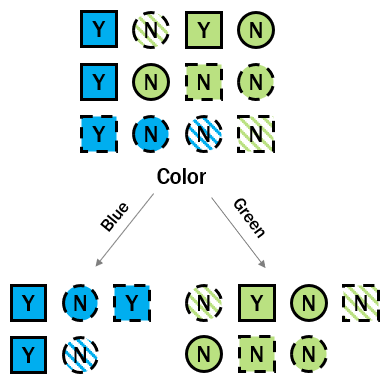
Du hast den ersten Schritt zur Messung des Informationsgewinns, den die Farbe liefert, abgeschlossen – du hast die Unordnung des Wurzelknotens berechnet. Jetzt musst du die Entropie der Kindknoten bestimmen, damit du prüfen kannst, ob die gemeinsame Unordnung der Kindknoten geringer ist als die Unordnung des Elternknotens. Wenn ja, hast du aus der in der Farbe enthaltenen Information etwas über den Status des Kreditausfalls gelernt.
Diese Übung ist Teil des Kurses
Dimensionsreduktion in R
Anleitung zur Übung
- Berechne die Klassenwahrscheinlichkeiten für den linken Split (blaue Seite).
- Berechne die Entropie des linken Splits mithilfe der Klassenwahrscheinlichkeiten.
- Berechne die Klassenwahrscheinlichkeiten für den rechten Split (grüne Seite).
- Berechne die Entropie des rechten Splits mithilfe der Klassenwahrscheinlichkeiten.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Calculate the class probabilities in the left split
p_left_yes <- ___
p_left_no <- ___
# Calculate the entropy of the left split
entropy_left <- -(___ * ___(___)) +
-(___ * ___(___))
# Calculate the class probabilities in the right split
p_right_yes <- ___
p_right_no <- ___
# Calculate the entropy of the right split
entropy_right <- -(___ * ___(___)) +
-(___ * ___(___))