Manufacturing Optimization: Score & Rank

Let's use the same discrete-event model of the wall clock factory and set up a "Score & Rank" optimization routine. For your convenience, the manufacturing process is summarized again in the table below. The information has been stored in a list of dictionaries named processes, with one dictionary per process. The keys of this dictionary correspond to the table column headers.

Table with process names and their duration statistics, namely mean and standard deviation.

The plot_results() method used to generate the plots in this exercise has been pre-loaded and is shown below.

def plot_results(objective_func):
    # Score
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.scatterplot(ax=axes[p], x=process_duration_all[:, p], y=objective_func, c=objective_func, cmap="turbo_r")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Duration [min]", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Objective function score")
    plt.show()

    # Rank
    index_sort = np.argsort(objective_func)
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.lineplot(ax=axes[p], x=np.linspace(0, NUM_SIMULATIONS, NUM_SIMULATIONS),
                     y=process_duration_all[index_sort, p], color="orchid")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Score-ranked scenarios", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Duration [min]")
    plt.show()

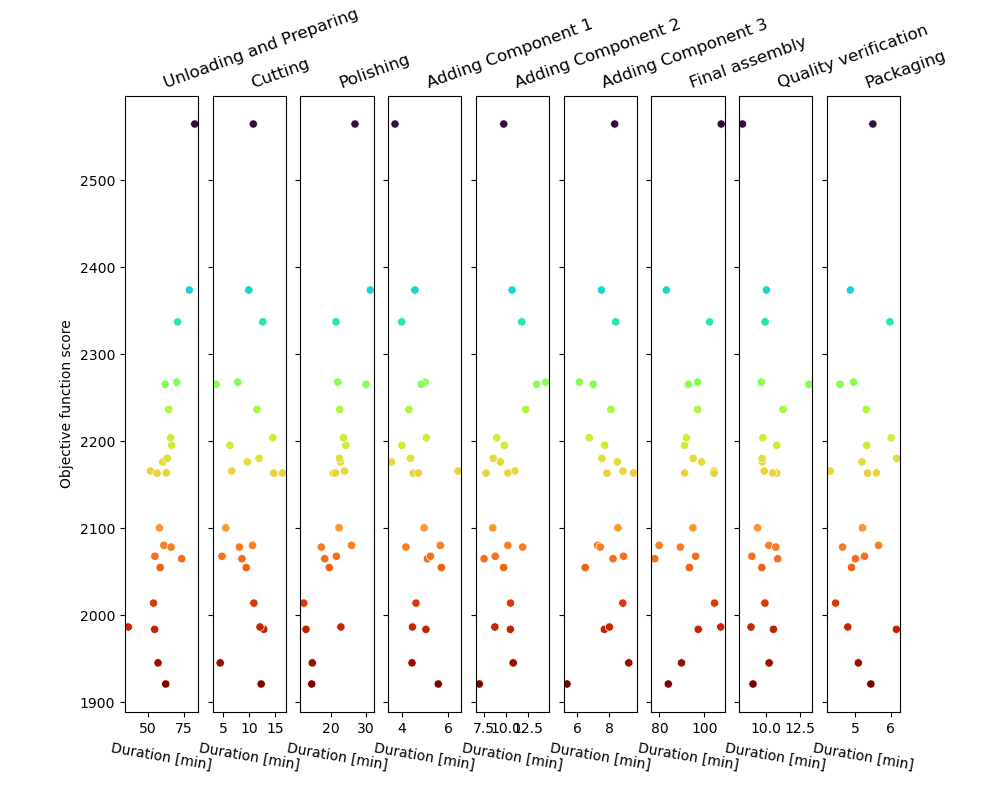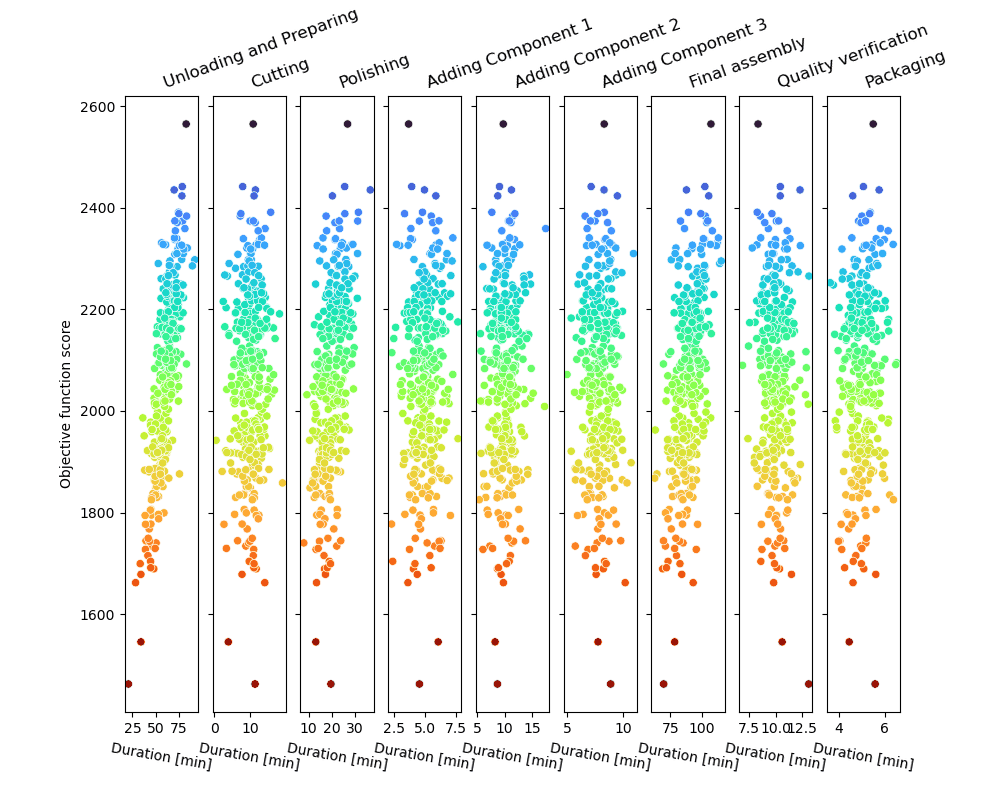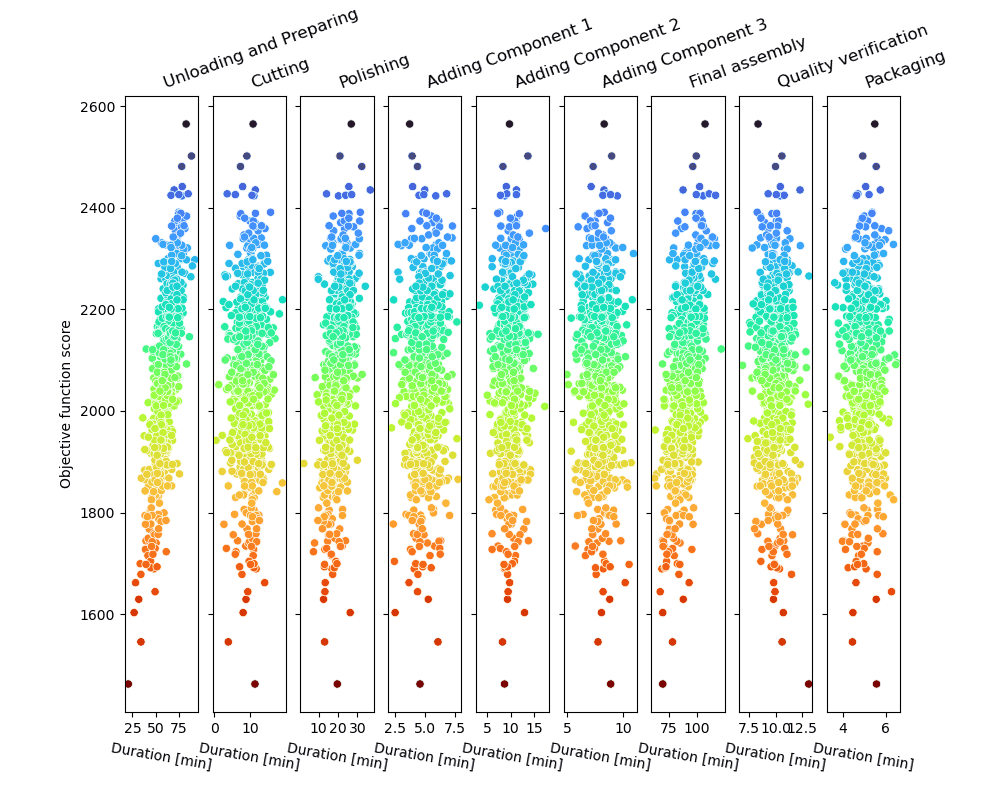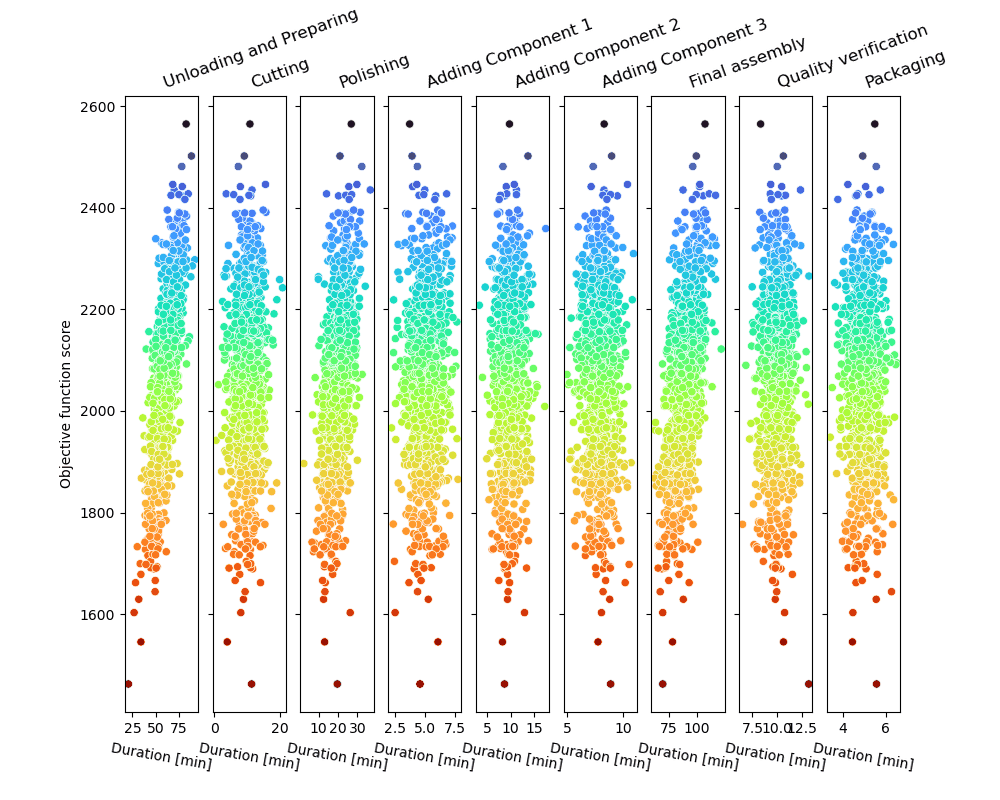
The Monte-Carlo sampling loop will produce a series of possible process trajectories and score them, as shown in the figure. Monte Carlo trajectories for different process scenario.

This exercise is part of the course

Discrete Event Simulation in Python

View Course

Exercise instructions

Add the score-contribution of each process, knowing that the duration of processes is stored in process_duration_all[s, p] and their respective weight in proc_p["score_weight_0_10"].
Set the for loop to run NUM_SIMULATIONS Monte-Carlo runs with s as the dummy variable.
Run the Monte Carlo engine stored in the function run_monte_carlo() (this will generate both the "score" and "rank" plots)

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

def objective_function_calc():
    objective_func = np.ones(NUM_SIMULATIONS)

    for s in range(NUM_SIMULATIONS):
        for p in range(len(processes)):
            proc_p = processes[p]
            
            # Add the score contribution of each process
            objective_func[s] += ____

    plot_results(objective_func)

def run_monte_carlo():

    # Set the for-loop to run NUM_SIMULATIONS Monte-Carlo runs 
    ____

        env = simpy.Environment()
        env.process(manufractoring_process(env, s))
        env.run()

    objective_function_calc()

# Run the Monte Carlo function
____

Edit and Run Code