Garment Production: Multi-processes and modularity

You have been asked to create a discrete-event model to help optimize a garment production factory situated in the Italian city of Milan, known as the fashion capital.

You are super excited and want to make sure you build a helpful and scalable model because you know that the garment industry is complex and involves many processes and resources, which you are still becoming familiar with.

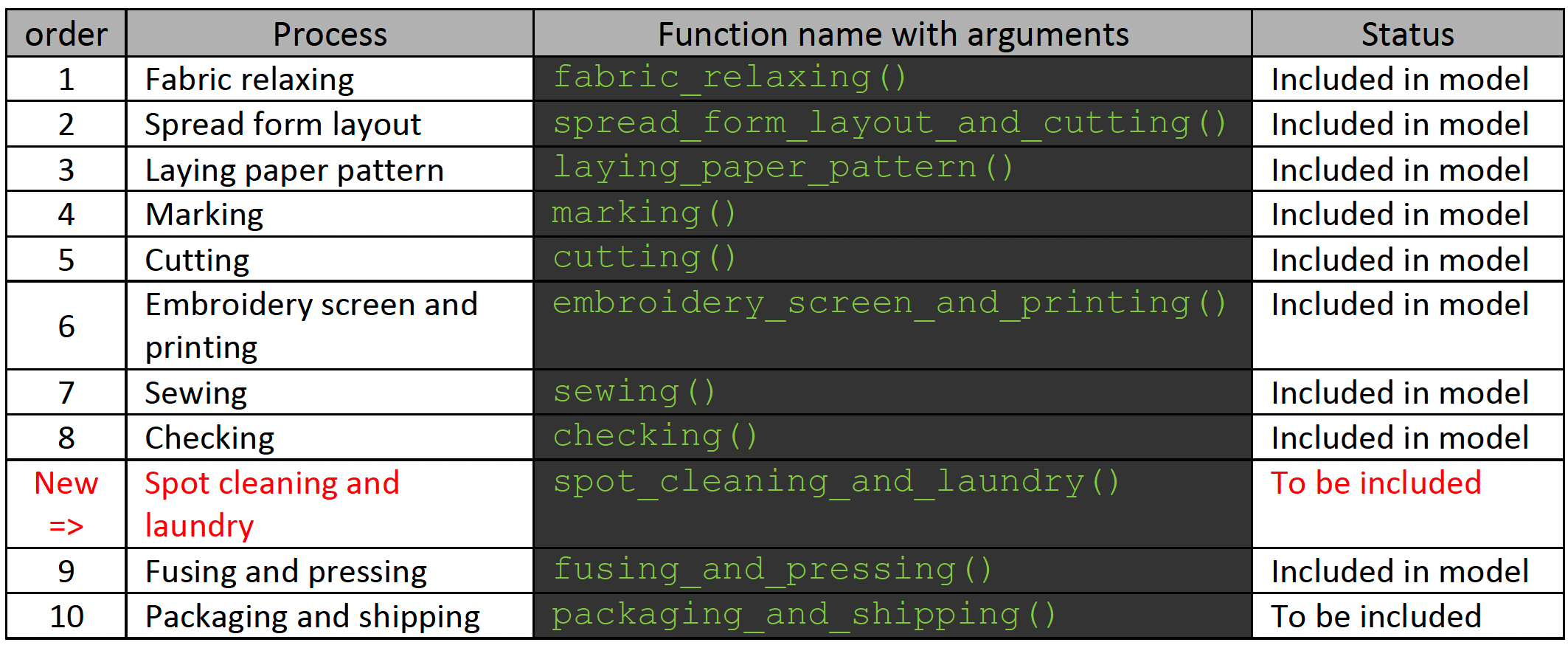
You did your research and came up with the list of processes shown in the table below. You were diligent and created a separate function for each process to make your model modular and allow it to grow in a controlled manner.

Now, you have received feedback from your manager, and you were told to include a new process in the model to account for "Spot cleaning and laundry", which should go between steps 8 and 9 (see the table row highlighted in red). The packages random and simpy have been imported.

Table with process names, respective functions, and information about whether the process has been incorporated in the model.

This exercise is part of the course

Discrete Event Simulation in Python

View Course

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Create a function for the new process
def ____(gen_type=None, gauss_mean=None, gauss_std=None, unif_start=None, unif_end=None):
  if gen_type == "gauss":
    duration = random.gauss(gauss_mean, gauss_std)
  elif gen_type == "uniform":
    duration = random.uniform(unif_start, unif_end)
  return duration

def all_processes(env, prod_line):

  with prod_line.request() as request:
    yield request

    t1 = fabric_relaxing(gen_type="gauss", gauss_mean=2*60, gauss_std=15)
    t2 = spread_form_layout(gen_type="gauss", gauss_mean=6, gauss_std=1)
    t3 = laying_paper_pattern(gen_type="uniform", unif_start=3, unif_end=0.5)
    t4 = marking(gen_type="gauss", gauss_mean=6, gauss_std=1)
    t5 = cutting(gen_type="gauss", gauss_mean=5, gauss_std=0.5)
    t6 = embroidery_screen_and_printing(gen_type="uniform", unif_start=10, unif_end=2)
    t7 = sewing(gen_type="gauss", gauss_mean=15, gauss_std=3)
    t8 = checking(gen_type="gauss", gauss_mean=2, gauss_std=0.5)

    # Add the new process
    tnew = ____

    # Account for the new process duration in the entire process duration
    total_duration = sum([t1, t2, t3, t4, t5, t6, t7, t8, ____, t9, t10])

    yield env.timeout(total_duration)

Edit and Run Code