Mauvaises distributions d’entrée

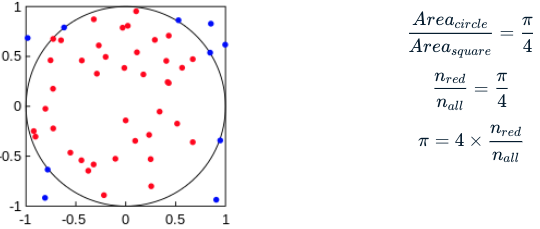
Vous allez continuer avec l’exemple de pi dans cet exercice : A graph of a circle inside a square with randomly sampled points

Que se passe-t-il si vous remplacez la loi de probabilité d’entrée, de la loi uniforme continue (random.uniform()) à la loi uniforme discrète (random.randint()) ? Vos résultats ne seront pas fiables, car random.randint() échantillonne des entiers discrets, tandis que random.uniform() échantillonne des nombres flottants continus.

Regardez bien la valeur de pi estimée par cette simulation. Comme la loi de probabilité choisie est incorrecte, l’estimation ne sera pas très précise ! Choisir les bonnes distributions de probabilité est essentiel pour les simulations de Monte Carlo. Nous détaillerons différentes distributions dans les leçons suivantes afin que vous vous sentiez à l’aise pour sélectionner la bonne par la suite.

random a déjà été importé pour vous.

Cet exercice fait partie du cours

Simulations de Monte Carlo en Python

Afficher le cours

Instructions

Échantillonnez les coordonnées x et y dans l’intervalle de -1 à 1 en utilisant random.randint() plutôt que la fonction correcte random.uniform() utilisée dans la vidéo.

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

n = 10000
circle_points = 0 
square_points = 0 
for i in range(n):
    # Sample the x and y coordinates from -1 to 1 using random.randint()
    x = ____
    y = ____
    dist_from_origin = x**2 + y**2
    if dist_from_origin <= 1:
        circle_points += 1
    square_points += 1
pi = 4 * circle_points / square_points
print(pi)

Modifier et exécuter le code