Effektstärke für Mittelwerte
Viele von Venture Capital finanzierte Unternehmen erhalten mehr als eine Finanzierungsrunde. Allgemein ist die zweite Runde größer als die erste. Wie stark beeinflusst die Rundennummer den durchschnittlichen Finanzierungsbetrag? Mit Cohen's d kannst du das quantifizieren.
Zur Erinnerung: Um Cohen's d zu berechnen, musst du zuerst die gepoolte Standardabweichung berechnen. Diese ist gegeben durch die Gleichung
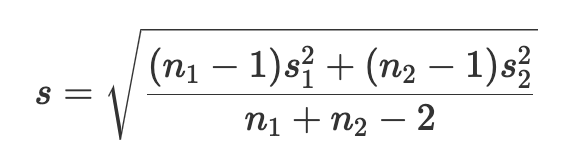
Cohen's d ergibt sich dann als:

Ein DataFrame mit Venture-Capital-Investitionen (investments_df) wurde für dich geladen, ebenso die Pakete pandas als pd, NumPy als np und stats aus SciPy. Die Spalte funding_total_usd zeigt die gesamte Finanzierung, die in dieser Runde erhalten wurde.
Diese Übung ist Teil des Kurses
Grundlagen der Inferenz in Python
Anleitung zur Übung
- Filtere
investments_df, umfunding_rounds1 und 2 jeweils separat auszuwählen. - Berechne die Standardabweichung und die Stichprobengröße jeder Runde.
- Berechne die gepoolte Standardabweichung zwischen den beiden Runden.
- Berechne Cohen's d mit den soeben ermittelten Größen.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Select all investments from rounds 1 and 2 separately
round1_df = investments_df[____['funding_rounds'] == ____]
round2_df = investments_df[____['funding_rounds'] == ____]
# Calculate the standard deviation of each round and the number of companies in each round
round1_sd = ____.std()
round2_sd = ____.std()
round1_n = ____.shape[0]
round2_n = ____.shape[0]
# Calculate the pooled standard deviation between the two rounds
pooled_sd = np.sqrt(((____ - 1) * ____ ** 2 + (____ - 1) *____ ** 2) / (____ + ____ - 2))
# Calculate Cohen's d
d = (____.mean() - ____.mean()) / ____