Take it easy: a simple life insurance
Cynthia wants to help her friend Ethan who is studying for the Long-Term Actuarial Mathematics exam organized by the Society of Actuaries. She explains him a very simple life insurance product: a product sold to \((20)\) that pays 10,000 EUR at the end of the year of death if death occurs at a given age \(30\). The figure illustrates how you should value this life insurance coverage.
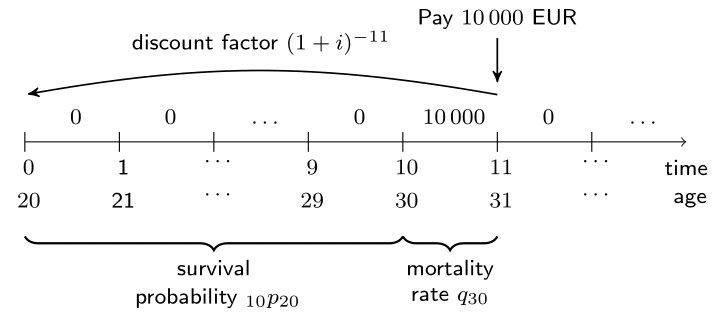
You can assume an interest rate \(i = 1\%\) and use the one-year survival probabilities px and mortality rates qx which have been preloaded.
This exercise is part of the course
Life Insurance Products Valuation in R
Exercise instructions
- Define
kpxas the 10-year survival probability of (20). - Assign the 10-year deferred mortality probability of (20) to
kqx. - Specify the discount factor that discounts a payment at the end of year 11 to the present moment at rate 1%.
- Calculate the EPV of the simple life insurance product by multiplying the benefit of 10,000 EUR with
discount_factorandkqx.
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# 10-year survival probability of (20)
kpx <- ___(___[(___):(___)])
kpx
# 10-year deferred mortality probability of (20)
kqx <- ___ * ___[___]
kqx
# Discount factor
discount_factor <- (1 + ___) ^ - ___
discount_factor
# EPV of the simple life insurance
___ * ___ * ___