Best of both worlds – the endowment insurance
Cynthia knows Miss Cathleen’s family and their financial situation quite well. Cynthia suggests her to think about retirement home expenses and to add a savings component to her policy that pays 80,000 EUR if she is alive at age 75. Miss Cathleen wants to finance this endowment insurance using constant premiums \(P\). The full setup of the life insurance plan is visualized in the following timeline.
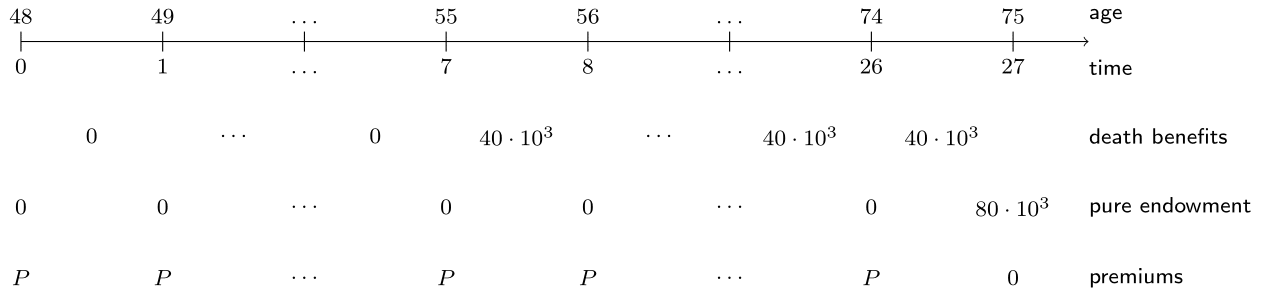
The survival probabilities px, the interest rate i and EPV_death_benefits, which you computed in the previous exercise, are available in your workspace. Now it is up to you to determine the premium level \(P\).
This exercise is part of the course
Life Insurance Products Valuation in R
Exercise instructions
- Determine the EPV of the pure endowment by multiplying the benefit of 80,000, the discount factor \((1 + i) ^ {-27}\) and the survival probability \(_{27}p_{48}\).
- Calculate the EPV of the premium pattern and assign the result to
EPV_rho. - Print the premium level \(P\) using the concept of actuarial equivalence.
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# Pure endowment
EPV_pure_endowment <- ___ * (1 + i) ^ - 27 * prod(px[(___):(___)])
EPV_pure_endowment
# Premium pattern
kpx <- c(___, cumprod(px[(___):(___)]))
discount_factors <- (___) ^ - (0:(length(kpx) - 1))
rho <- rep(1, length(kpx))
EPV_rho <- ___
EPV_rho
# Premium level
(___ + ___) / ___