Evitando mínimos locais
No exercício anterior, você viu como é fácil ficar preso em mínimos locais. Tínhamos um problema simples de otimização em uma variável e, ainda assim, o gradiente descendente não encontrou o mínimo global quando foi preciso atravessar mínimos locais antes. Uma forma de evitar esse problema é usar momentum, que permite ao otimizador “atravessar” mínimos locais. Vamos usar novamente a função de perda do exercício anterior, que já foi definida e está disponível para você como loss_function().
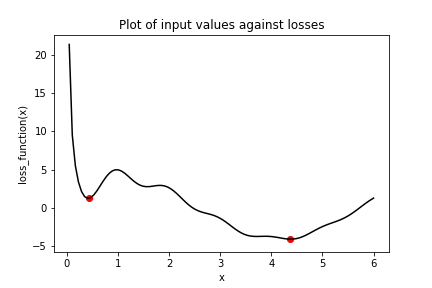
Vários otimizadores no tensorflow têm um parâmetro de momentum, incluindo SGD e RMSprop. Neste exercício, você vai usar RMSprop. Observe que x_1 e x_2 foram inicializados com o mesmo valor desta vez. Além disso, keras.optimizers.RMSprop() também já foi importado para você a partir de tensorflow.
Este exercício faz parte do curso
Introdução ao TensorFlow em Python
Instruções do exercício
- Defina a operação
opt_1para usar taxa de aprendizado (learning_rate) de 0.01 e momentum de 0.99. - Defina
opt_2para usar o otimizador RMSprop (root mean square propagation) com taxa de aprendizado de 0.01 e momentum de 0.00. - Defina a operação de minimização para
opt_2. - Imprima
x_1ex_2como arrays donumpy.
Exercício interativo prático
Experimente este exercício completando este código de exemplo.
# Initialize x_1 and x_2
x_1 = Variable(0.05,float32)
x_2 = Variable(0.05,float32)
# Define the optimization operation for opt_1 and opt_2
opt_1 = keras.optimizers.RMSprop(learning_rate=____, momentum=____)
opt_2 = ____
for j in range(100):
opt_1.minimize(lambda: loss_function(x_1), var_list=[x_1])
# Define the minimization operation for opt_2
____
# Print x_1 and x_2 as numpy arrays
print(____, ____)