Wrong deterministic calculation

In this exercise and the next, you'll play around with the pi calculations from the video to further understand the importance of each step in the simulation process.

Recall that the simulation to find pi generates random points \((x, y)\) where \(x\) and \(y\) are between -1 and 1, as shown in the graph below.

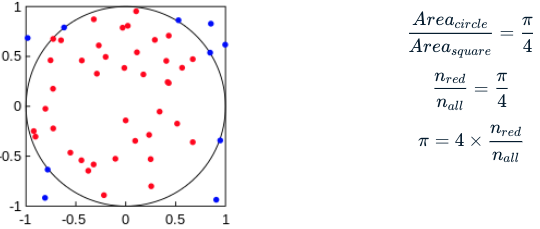
A graph of a circle inside a square with randomly sampled points

What if you incorrectly changed the deterministic calculation where you check whether a point should be added to circle_points? How will this affect the final result? You'll see from the wacky value you get for pi that correctly specifying deterministic calculations is essential for Monte Carlo simulations!

random has been imported for you.

Deze oefening maakt deel uit van de cursus

Monte Carlo Simulations in Python

Cursus bekijken

Oefeninstructies

Increment circle_points for any point with a distance from origin of less than 0.75 (rather than a distance of one as demonstrated in the video).

Praktische interactieve oefening

Probeer deze oefening eens door deze voorbeeldcode in te vullen.

n = 10000
circle_points = 0 
square_points = 0 
for i in range(n):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    dist_from_origin = x**2 + y**2
    # Increment circle_points for any point with a distance from origin of less than .75
    if ____:
        circle_points += 1
    square_points += 1
pi = 4 * circle_points / square_points
print(pi)

Code bewerken en uitvoeren