Otimização na Manufatura: Score & Rank

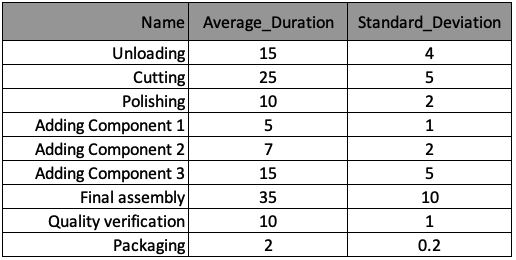
Vamos usar o mesmo modelo de eventos discretos da fábrica de relógios de parede e configurar uma rotina de otimização "Score & Rank". Para sua conveniência, o processo de manufatura está resumido novamente na tabela abaixo. As informações foram armazenadas em uma lista de dicionários chamada processes, com um dicionário por processo. As chaves desse dicionário correspondem aos cabeçalhos das colunas da tabela.

Table with process names and their duration statistics, namely mean and standard deviation.

O método plot_results() usado para gerar os gráficos neste exercício já foi carregado e é mostrado abaixo.

def plot_results(objective_func):
    # Score
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.scatterplot(ax=axes[p], x=process_duration_all[:, p], y=objective_func, c=objective_func, cmap="turbo_r")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Duration [min]", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Objective function score")
    plt.show()

    # Rank
    index_sort = np.argsort(objective_func)
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.lineplot(ax=axes[p], x=np.linspace(0, NUM_SIMULATIONS, NUM_SIMULATIONS),
                     y=process_duration_all[index_sort, p], color="orchid")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Score-ranked scenarios", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Duration [min]")
    plt.show()

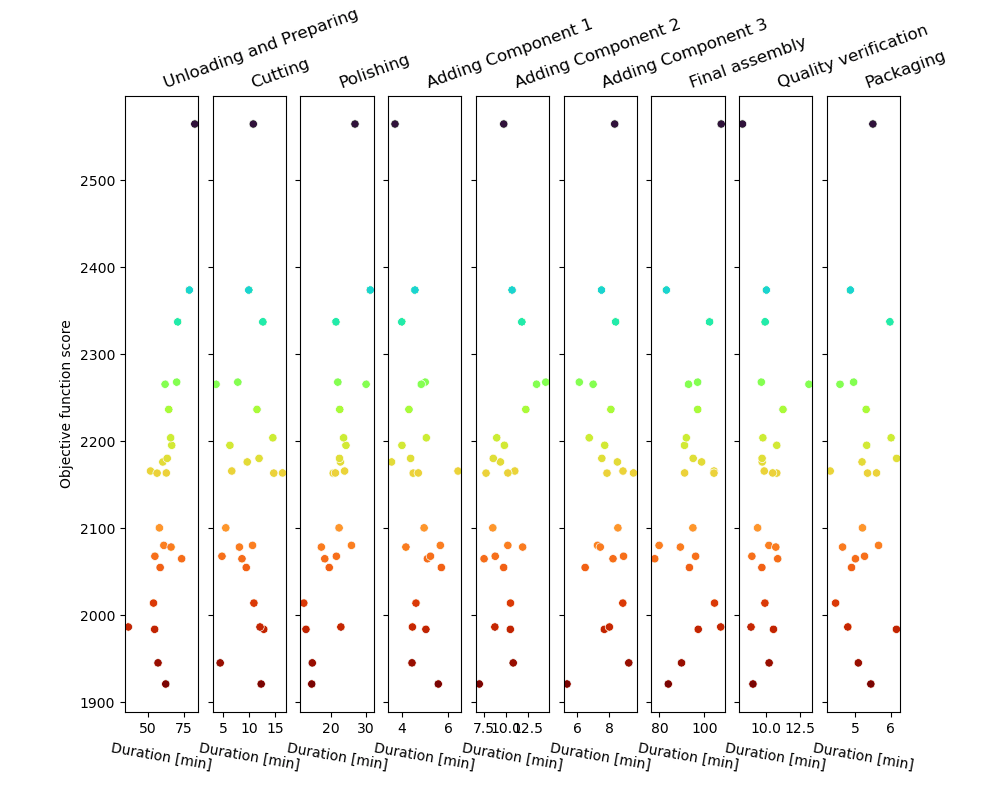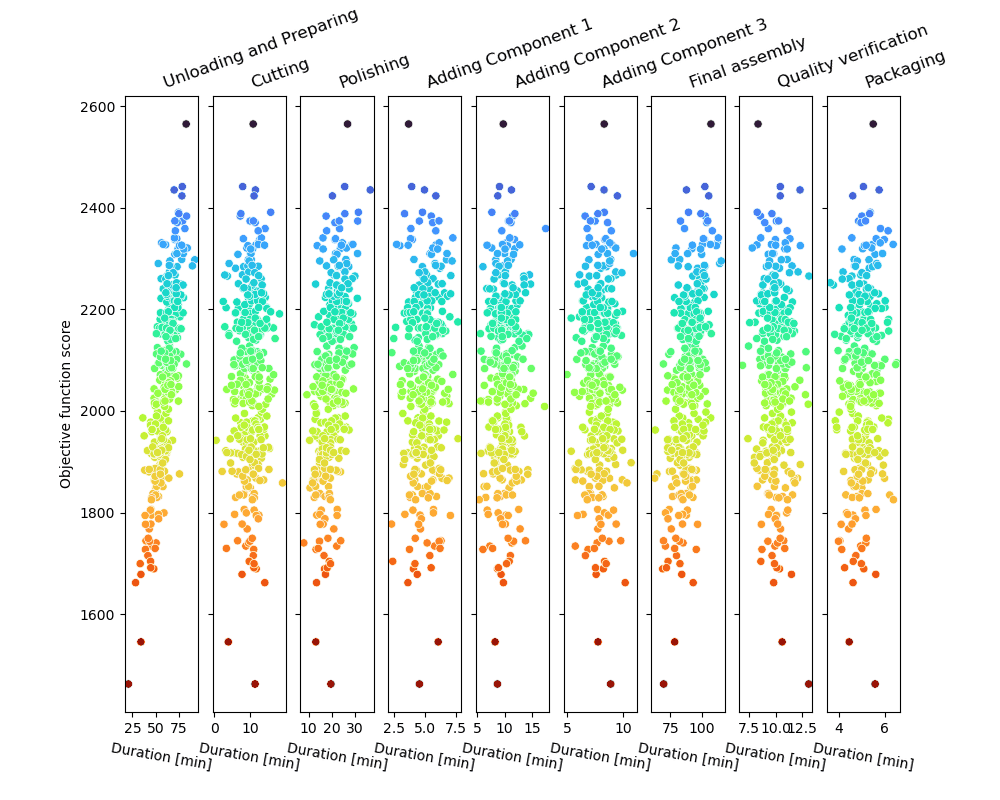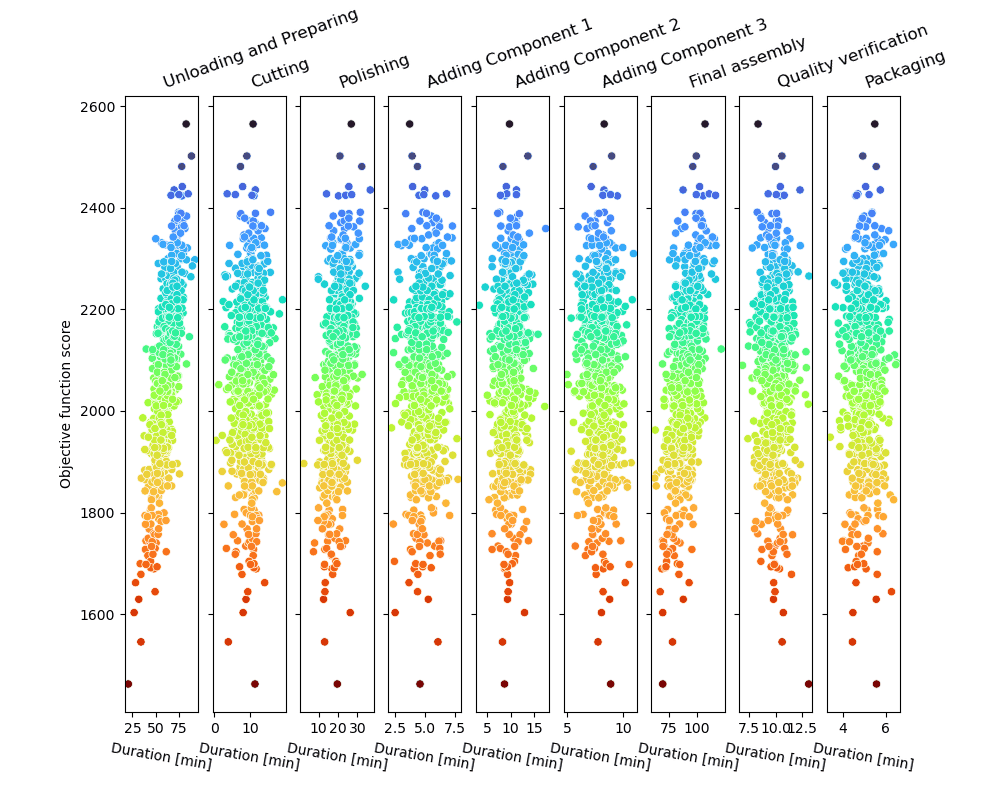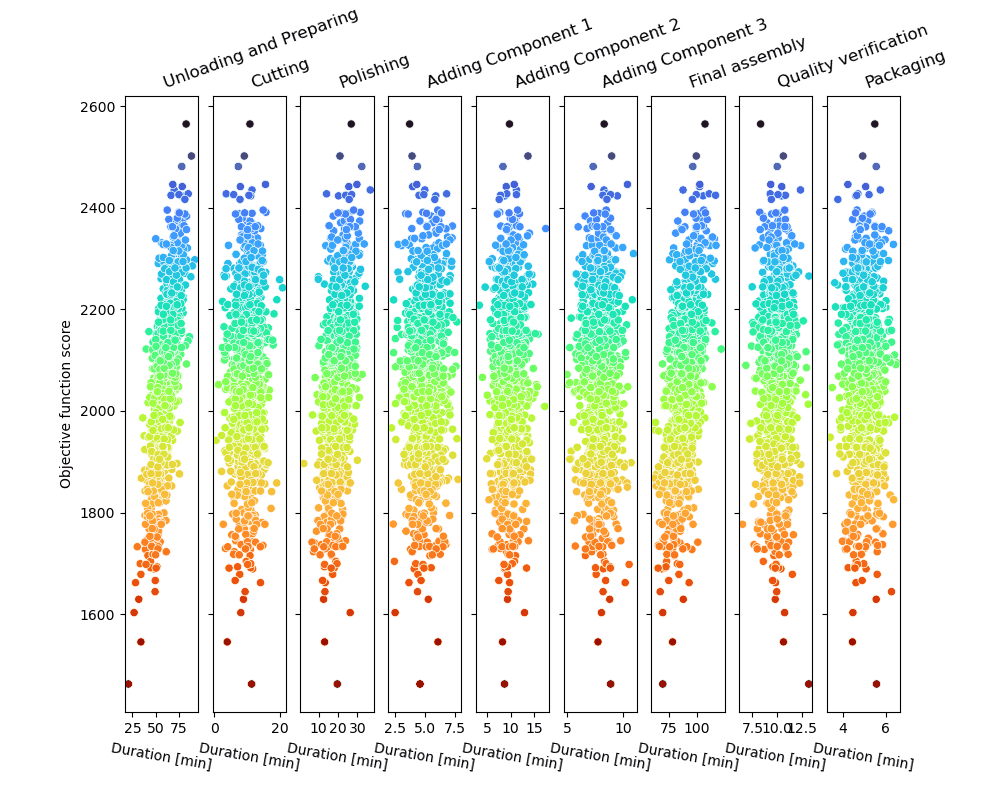
O loop de amostragem de Monte Carlo produzirá uma série de trajetórias de processo possíveis e as pontuará, como mostrado na figura. Monte Carlo trajectories for different process scenario.

Este exercício faz parte do curso

Simulação de Eventos Discretos em Python

Ver curso

Instruções do exercício

Some a contribuição de pontuação de cada processo, sabendo que a duração dos processos está armazenada em process_duration_all[s, p] e seus respectivos pesos em proc_p["score_weight_0_10"].
Configure o laço for para executar NUM_SIMULATIONS rodadas de Monte Carlo com s como variável auxiliar.
Execute o mecanismo de Monte Carlo armazenado na função run_monte_carlo() (isso vai gerar os gráficos de "score" e "rank")

Exercício interativo prático

Experimente este exercício completando este código de exemplo.

def objective_function_calc():
    objective_func = np.ones(NUM_SIMULATIONS)

    for s in range(NUM_SIMULATIONS):
        for p in range(len(processes)):
            proc_p = processes[p]
            
            # Add the score contribution of each process
            objective_func[s] += ____

    plot_results(objective_func)

def run_monte_carlo():

    # Set the for-loop to run NUM_SIMULATIONS Monte-Carlo runs 
    ____

        env = simpy.Environment()
        env.process(manufractoring_process(env, s))
        env.run()

    objective_function_calc()

# Run the Monte Carlo function
____

Editar e executar o código