Produção de Vestuário: Multietapas e modularidade
Você foi convidado a criar um modelo de eventos discretos para ajudar a otimizar uma fábrica de produção de vestuário localizada em Milão, na Itália, conhecida como a capital da moda.
Você está super animado e quer garantir que vai construir um modelo útil e escalável, porque sabe que a indústria do vestuário é complexa e envolve muitos processos e recursos, com os quais você ainda está se familiarizando.
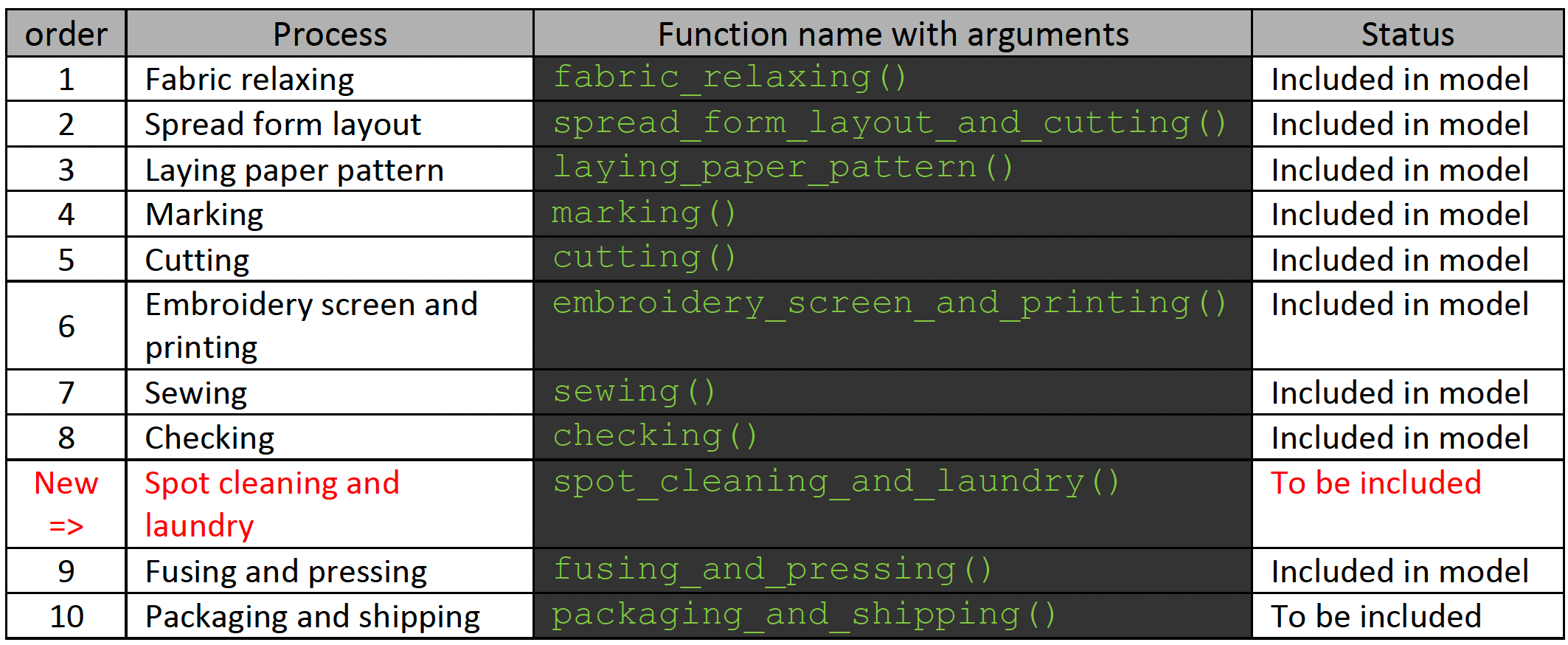
Você fez sua pesquisa e elaborou a lista de processos mostrada na tabela abaixo. Você foi cuidadoso e criou uma função separada para cada processo para tornar seu modelo modular e permitir que ele cresça de maneira controlada.
Agora, você recebeu o feedback da sua gerência e foi orientado a incluir um novo processo no modelo para contemplar "Spot cleaning and laundry", que deve ficar entre as etapas 8 e 9 (veja a linha da tabela destacada em vermelho). Os pacotes random e simpy já foram importados.
Este exercício faz parte do curso
Simulação de Eventos Discretos em Python
Exercício interativo prático
Experimente este exercício completando este código de exemplo.
# Create a function for the new process
def ____(gen_type=None, gauss_mean=None, gauss_std=None, unif_start=None, unif_end=None):
if gen_type == "gauss":
duration = random.gauss(gauss_mean, gauss_std)
elif gen_type == "uniform":
duration = random.uniform(unif_start, unif_end)
return duration
def all_processes(env, prod_line):
with prod_line.request() as request:
yield request
t1 = fabric_relaxing(gen_type="gauss", gauss_mean=2*60, gauss_std=15)
t2 = spread_form_layout(gen_type="gauss", gauss_mean=6, gauss_std=1)
t3 = laying_paper_pattern(gen_type="uniform", unif_start=3, unif_end=0.5)
t4 = marking(gen_type="gauss", gauss_mean=6, gauss_std=1)
t5 = cutting(gen_type="gauss", gauss_mean=5, gauss_std=0.5)
t6 = embroidery_screen_and_printing(gen_type="uniform", unif_start=10, unif_end=2)
t7 = sewing(gen_type="gauss", gauss_mean=15, gauss_std=3)
t8 = checking(gen_type="gauss", gauss_mean=2, gauss_std=0.5)
# Add the new process
tnew = ____
# Account for the new process duration in the entire process duration
total_duration = sum([t1, t2, t3, t4, t5, t6, t7, t8, ____, t9, t10])
yield env.timeout(total_duration)