Effect size for means
Many venture capital-backed companies receive more than one round of funding. In general, the second round is bigger than the first. Just how much of an effect does the round number have on the average funding amount? You can use Cohen's d to quantify this.
Recall that, to calculate Cohen's d, you need to first calculate the pooled standard deviation. That is given by the equation
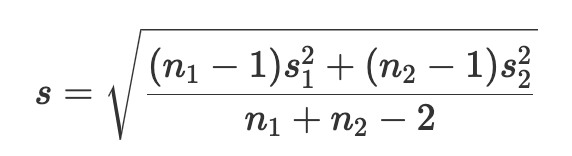
Cohen's d is then given by:

A DataFrame of venture capital investments (investments_df) has been loaded for you, as have the packages pandas as pd, NumPy as np and stats from SciPy. The column funding_total_usd shows the total funding received in that round.
This exercise is part of the course
Foundations of Inference in Python
Exercise instructions
- Filter
investments_dfto selectfunding_rounds1 and 2 separately. - Calculate the standard deviation and sample size of each round.
- Calculate the pooled standard deviation between the two rounds.
- Calculate Cohen's d using the terms you just calculated.
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# Select all investments from rounds 1 and 2 separately
round1_df = investments_df[____['funding_rounds'] == ____]
round2_df = investments_df[____['funding_rounds'] == ____]
# Calculate the standard deviation of each round and the number of companies in each round
round1_sd = ____.std()
round2_sd = ____.std()
round1_n = ____.shape[0]
round2_n = ____.shape[0]
# Calculate the pooled standard deviation between the two rounds
pooled_sd = np.sqrt(((____ - 1) * ____ ** 2 + (____ - 1) *____ ** 2) / (____ + ____ - 2))
# Calculate Cohen's d
d = (____.mean() - ____.mean()) / ____