Using pre-order traversal with Polish notation

Expression trees are a kind of binary tree that represent arithmetic expressions:

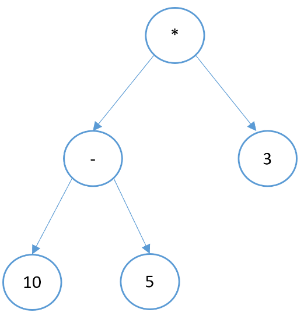
Graphical representation of a binary tree that has arithmetic expressions.

By applying in-order traversal to an expression tree, you can obtain the infix notation. This notation for the given tree will be (10-5)*3.

By applying pre-order traversal to an expression tree, you can obtain the prefix notation, aka Polish notation, where the operator appears before its operands. This notation for the given tree will be *-10 5 3.

By applying post-order traversal to an expression tree, you can obtain the postfix notation, aka reverse Polish notation, where the operator appears after its operands. This notation for the given tree will be 10 5- 3*.

Code the pre-order traversal so that you can obtain the prefix notation of this expression tree.

Deze oefening maakt deel uit van de cursus

Data Structures and Algorithms in Python

Cursus bekijken

Oefeninstructies

Check if current_node exists.
Print the value of the current_node.
Call the pre_order() function recursively on the appropriate halves of the tree.

Praktische interactieve oefening

Probeer deze oefening eens door deze voorbeeldcode in te vullen.

import queue

class ExpressionTree:
  def __init__(self):
    self.root = None

  def pre_order(self, current_node):
    # Check if current_node exists
    ____:
      # Print the value of the current_node
      ____
      # Call pre_order recursively on the appropriate half of the tree
      ____
      ____
          
et = CreateExpressionTree()
et.pre_order(et.root)

Code bewerken en uitvoeren