Optimización de fabricación: Score & Rank

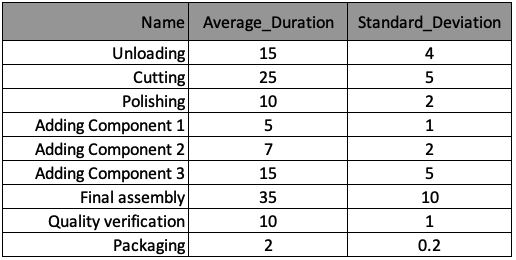
Vamos a usar el mismo modelo de eventos discretos de la fábrica de relojes de pared y a configurar una rutina de optimización "Score & Rank". Para tu comodidad, el proceso de fabricación se resume de nuevo en la tabla de abajo. La información se ha almacenado en una lista de diccionarios llamada processes, con un diccionario por proceso. Las claves de cada diccionario corresponden a los encabezados de columna de la tabla.

Table with process names and their duration statistics, namely mean and standard deviation.

El método plot_results() usado para generar las gráficas en este ejercicio ya está precargado y se muestra a continuación.

def plot_results(objective_func):
    # Score
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.scatterplot(ax=axes[p], x=process_duration_all[:, p], y=objective_func, c=objective_func, cmap="turbo_r")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Duration [min]", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Objective function score")
    plt.show()

    # Rank
    index_sort = np.argsort(objective_func)
    fig, axes = plt.subplots(1, len(processes), sharey=True, figsize=(10, 8))
    for p in range(len(processes)):
        sns.lineplot(ax=axes[p], x=np.linspace(0, NUM_SIMULATIONS, NUM_SIMULATIONS),
                     y=process_duration_all[index_sort, p], color="orchid")
        axes[p].set_title(processes[p]["Name"], rotation = 20, horizontalalignment='left')
        axes[p].set_xlabel("Score-ranked scenarios", rotation = -10)
        axes[p].grid()
    axes[0].set_ylabel("Duration [min]")
    plt.show()

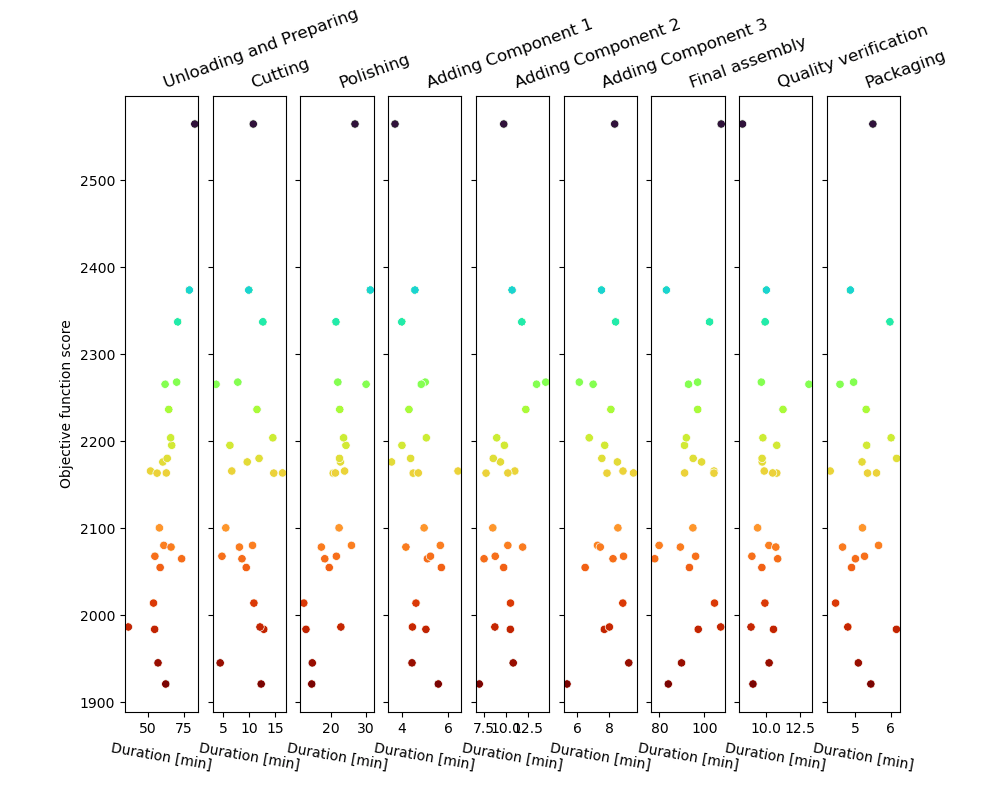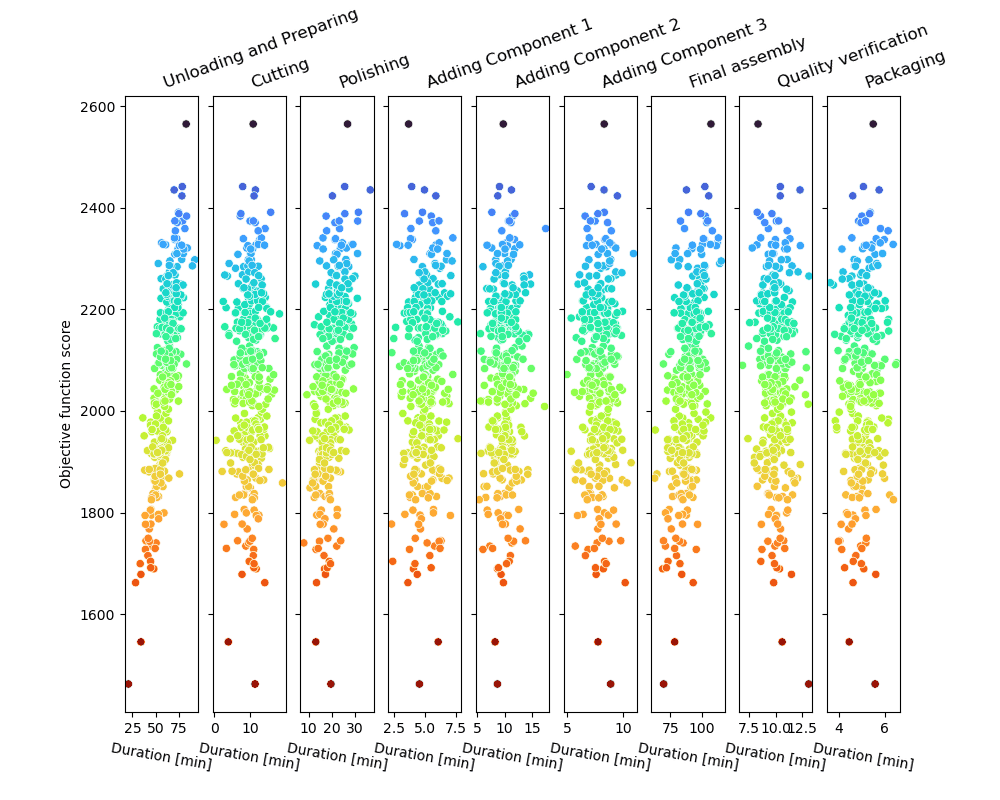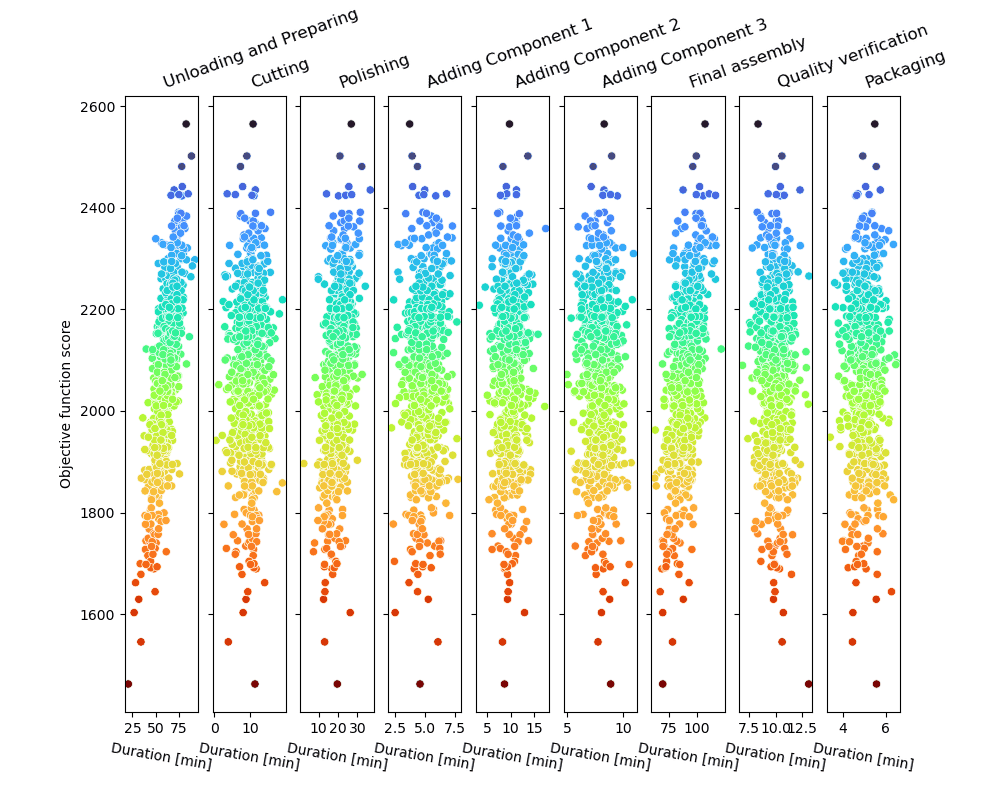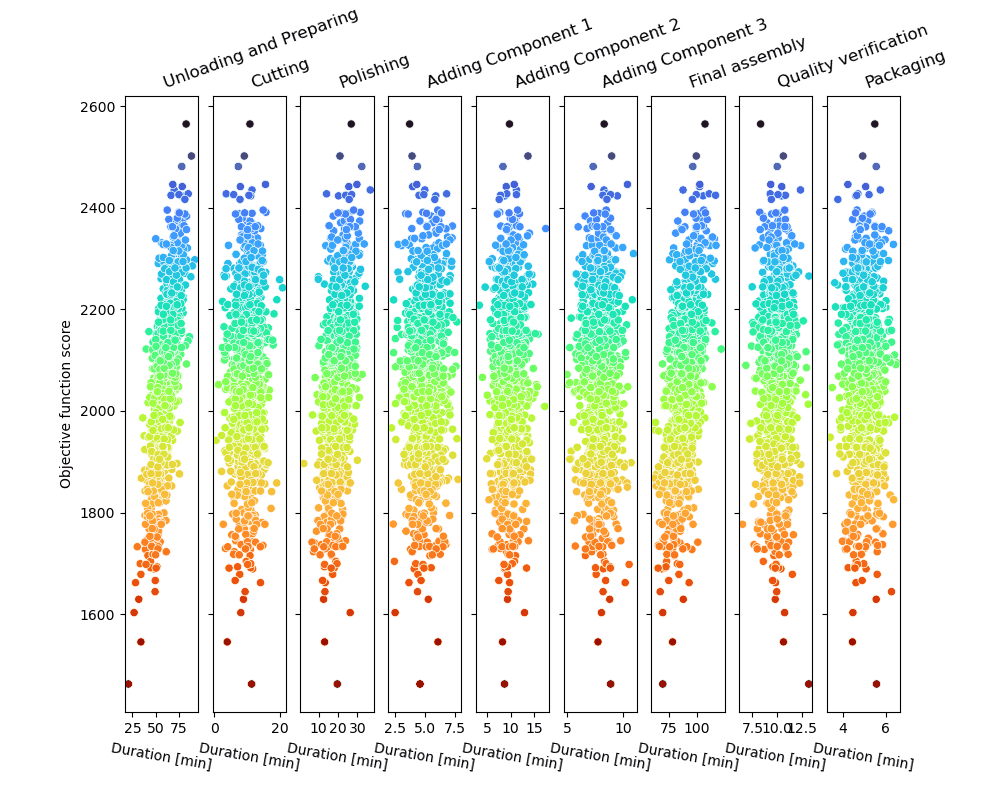
El bucle de muestreo Monte Carlo producirá una serie de trayectorias de proceso posibles y las puntuará, como se muestra en la figura. Monte Carlo trajectories for different process scenario.

Este ejercicio forma parte del curso

Simulación de eventos discretos en Python

Ver curso

Instrucciones del ejercicio

Añade la contribución a la puntuación de cada proceso, sabiendo que la duración de los procesos está en process_duration_all[s, p] y su peso correspondiente en proc_p["score_weight_0_10"].
Configura el bucle for para ejecutar NUM_SIMULATIONS ejecuciones de Monte Carlo usando s como variable muda.
Ejecuta el motor de Monte Carlo guardado en la función run_monte_carlo() (esto generará las gráficas de "score" y "rank")

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

def objective_function_calc():
    objective_func = np.ones(NUM_SIMULATIONS)

    for s in range(NUM_SIMULATIONS):
        for p in range(len(processes)):
            proc_p = processes[p]
            
            # Add the score contribution of each process
            objective_func[s] += ____

    plot_results(objective_func)

def run_monte_carlo():

    # Set the for-loop to run NUM_SIMULATIONS Monte-Carlo runs 
    ____

        env = simpy.Environment()
        env.process(manufractoring_process(env, s))
        env.run()

    objective_function_calc()

# Run the Monte Carlo function
____

Editar y ejecutar código