Finding outliers using IQR
Outliers can have big effects on statistics like mean, as well as statistics that rely on the mean, such as variance and standard deviation. Interquartile range, or IQR, is another way of measuring spread that's less influenced by outliers. IQR is also often used to find outliers. If a value is less than \(\text{Q1} - 1.5 \times \text{IQR}\) or greater than \(\text{Q3} + 1.5 \times \text{IQR}\), it's considered an outlier. In fact, this is how the lengths of the whiskers in a matplotlib box plot are calculated.
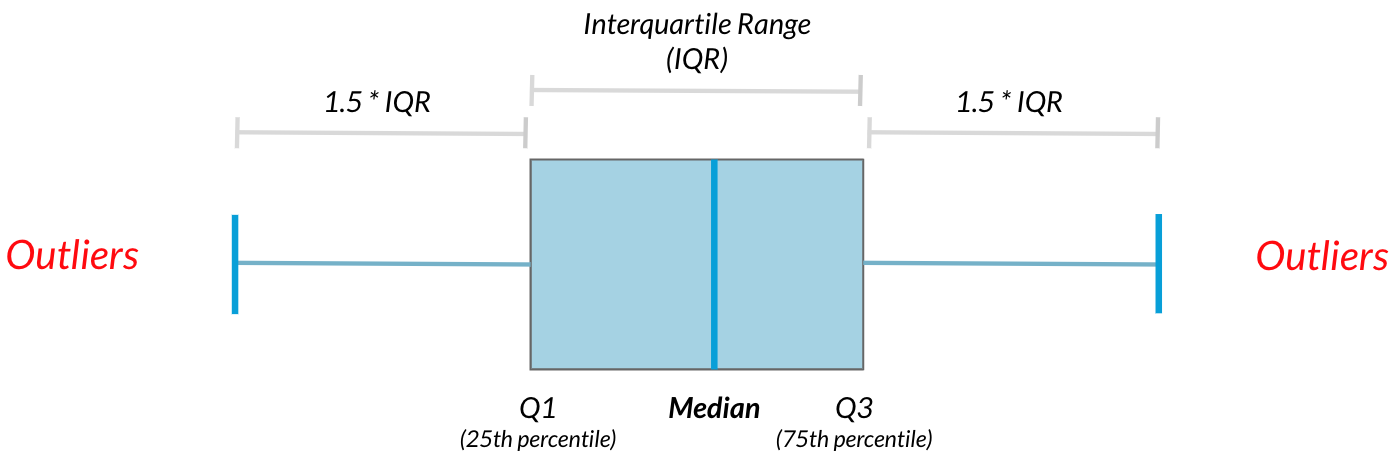
In this exercise, you'll calculate IQR and use it to find some outliers. pandas as pd and numpy as np are loaded and food_consumption is available.
This exercise is part of the course
Introduction to Statistics in Python
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# Calculate total co2_emission per country: emissions_by_country
emissions_by_country = ____
print(emissions_by_country)