Exercise

Traveling salesman problem (TSP)

The Traveling Salesman Problem (TSP) is a popular problem and has applications is logistics. In the TSP a salesman is given a list of cities, and the distance between each pair. He is looking for the shortest route going from the origin through all points before going back to the origin city again. This is a computationally difficult problem to solve but Miller-Tucker-Zemlin (MTZ) showed it can be completed using Integer Linear Programing. In this exercise you are going to define the objective and some constraints for of the TSP for a small dataset with 15 cities (see the image below). Your goal is to try out using LpVariable.dicts with list comprehension.

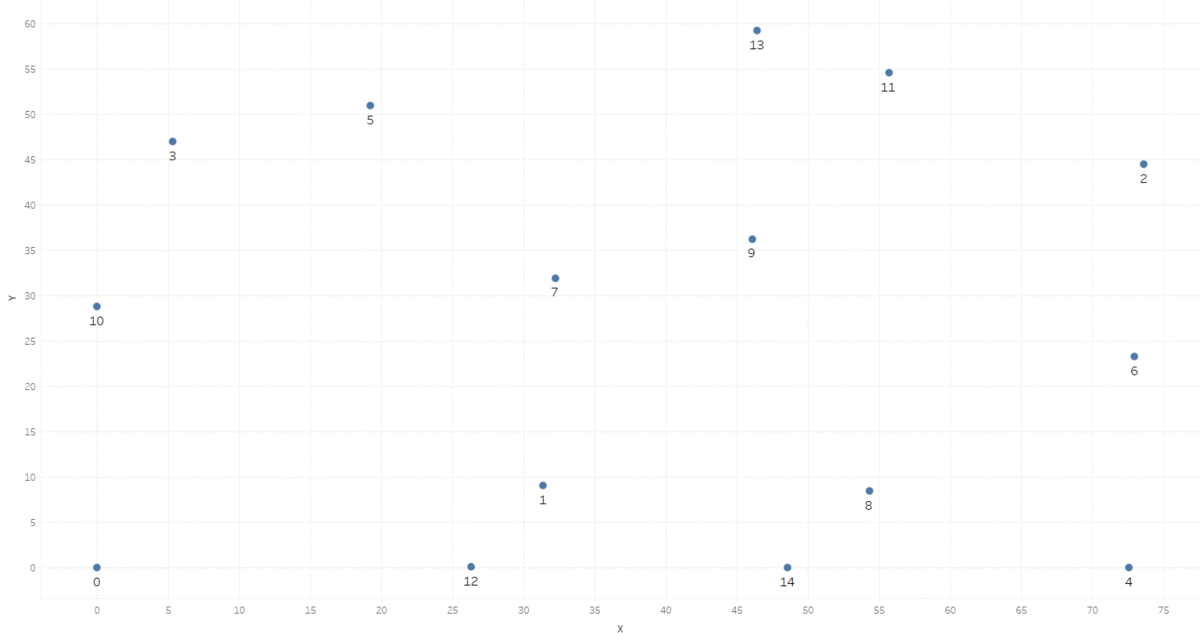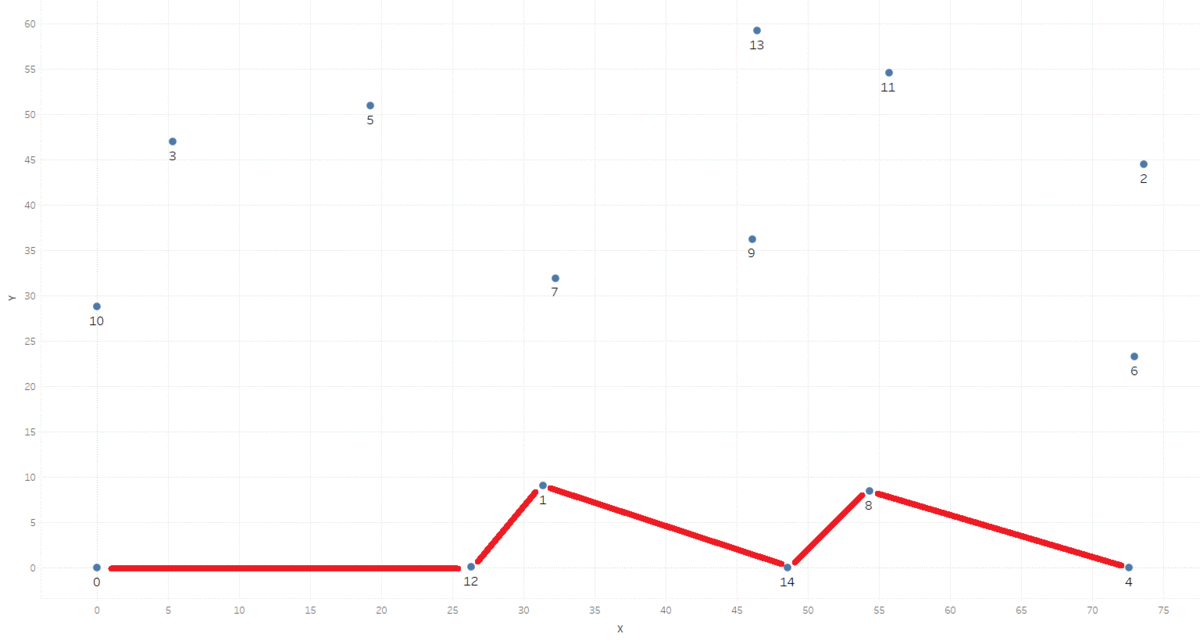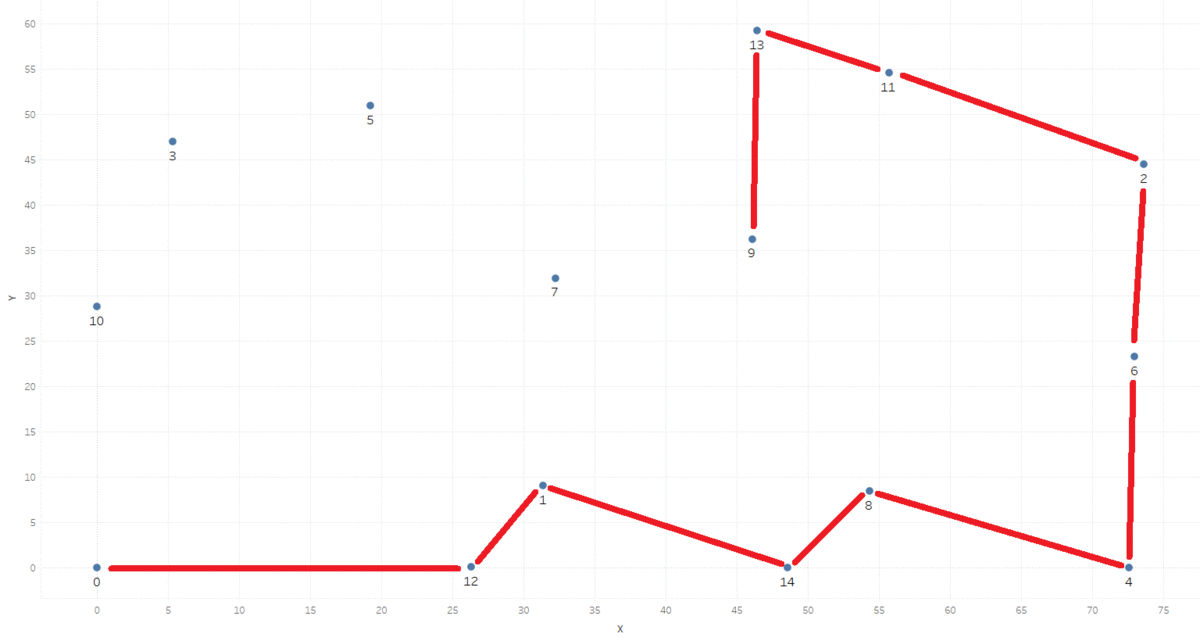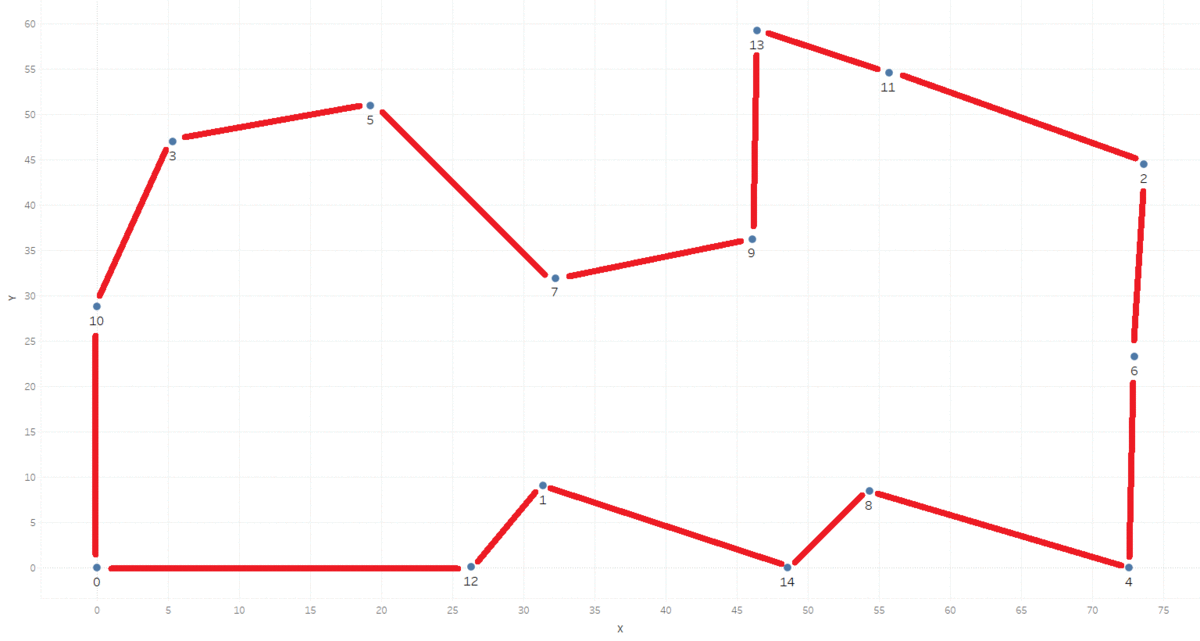
Photo of Cities

Three Python variables n, cities, and dist have been created for you \(^{1}\). The n variable is the number of cities, cities is a list of the cities numbered and dist is a pandas DataFrame with the pairwise distance between each city. You can explore them in the console. Additionally, the model has been initialized for you.

\(^{1}\) Dataset come from Gerhard Reinelt,TSPLIB - A Traveling Salesman Problem Library, ORSA Journal on Computing,

Instructions 1/3

undefined XP
    1
    2
    3
  • Use LpVariable.dicts to create a dictionary x holding binary variables for each city to city pair, and to create a dictionary u holding an integer LpVariable for each city.