Exercise

Uniform distribution

Questions related to the continuous uniform distribution come up during interviews because the calculations associated with this distribution are relatively straightforward.

A random variable is usually denoted as \(X\) and a continuous uniform distribution on a range \([a, b]\) is denoted as \(U(a, b)\).

Recall that punif(q = k, min = a, max = b) calculates \(P(X \le k)\) for \(X \sim U(a, b)\).

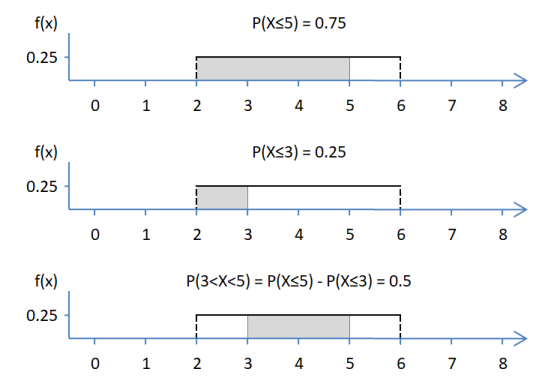
You can derive the probability that a random variable falls into a range as a difference of the two cumulative probabilities: \(P(j < X < k) = P(X \le k) - P(X \le j)\)

See the example below for \(X \sim U(2, 6)\):

Instructions 1/3

undefined XP
    1
    2
    3

Question

What is the probability that a random variable from the continuous uniform distribution on the range \([1, 10]\) falls into the range \([4, 7]\)?

Possible answers