1. Learn
    2. /
  2. Courses
    3. /
  3. Practicing Statistics Interview Questions in R

Exercise

Binomial distribution

In the previous exercise, you've modeled the Bernoulli trials. The binomial distribution is the sum of the number of successful outcomes in a set of Bernoulli trials.

The notation of the binomial distribution is \(B(n, p)\), where \(n\) is the number of experiments, and \(p\) is the probability of a success.

For this exercise, consider 10 consecutive fair coin flips. You've bet for tails and consider this outcome of a coin flip as a success.

Recall that:

  • dbinom(x = k, size = n, prob = p) calculates \(P(X = k)\) for \(X \sim B(n, p)\),
  • pbinom(q = k, size = n, prob = p) calculates \(P(X \le k)\) for \(X \sim B(n, p)\).

Remember that for discrete distributions that take on whole numbers: \(P(X \ge k) = 1 - P(X \le k-1)\).

For example:

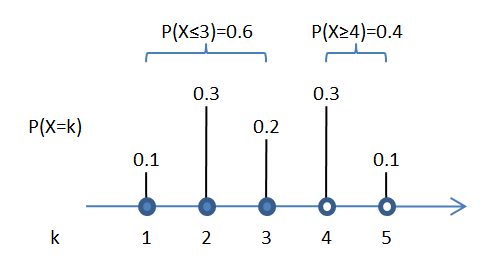
So, \(P(X \ge 4) = 1 - P(X \le 3)\).

Instructions

100 XP
  • Assign the probability of getting exactly 6 tails to six_tails and print the result.
  • Assign the probability of getting 7 or less tails to seven_or_less and print the result.
  • Assign the probability of getting 5 or more tails to five_or_more and print the result.