Simple imputation
As you saw in the last exercise, deleting data can reduce your dataset by too much. In an interview context, this can lead to biased results of your machine learning model.
A more dynamic way of handling missing values is by imputing them. There are a variety of ways of doing this in python, but in this exercise you will be using the SimpleImputer() function from the sklearn.impute module on loan_data.
You will then use pandas and numpy to convert the imputed dataset into a DataFrame.
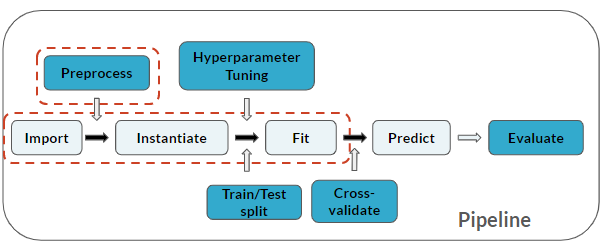
Note that 2 steps are now added to the pipeline, Instantiate and Fit:
This exercise is part of the course
Practicing Machine Learning Interview Questions in Python
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# Import imputer module
from sklearn.impute import SimpleImputer
# Subset numeric features: numeric_cols
numeric_cols = ____.____(include=[____.____])