Anywhere, anytime?

Reflecting upon her spending pattern, Cynthia wonders how much money she would collect if she puts her money on a bank account instead of spending it on downloads and concert tickets. To this end, you will calculate the value of the cash flows at a future point in time, using an appropriate discount function.

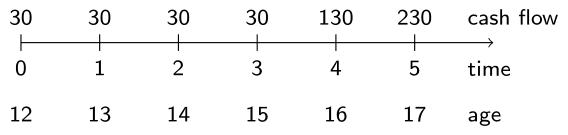
Cynthia's spending pattern is shown above. The cash_flows vector, which you defined in the first exercise, has been preloaded into your workspace. The interest rate is still 2%.

This exercise is part of the course

Life Insurance Products Valuation in R

View Course

Exercise instructions

Define the function discount() which computes the value at time \(s\) of 1 EUR paid at time \(t\).
Use discount() to compute the present value of the cash_flows at times 0 to 5. This should match your earlier result, namely 444.93 EUR.
Print the value of the cash flow vector when Cynthia turns 18 in 6 years from now.
Compute the accumulated value of the cash flow vector at time 6 in a different way. This time convert the present_value at time 0 to the value at time 6.

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Define the discount function v
discount <- function(s, t, i = 0.02) {
  (1 + ___) ^ - (___ - ___)
}

# Calculate the present value
present_value <- sum(cash_flows * discount(___, ___))
present_value

# Calculate the value at time 6
sum(cash_flows * discount(___, ___))

# Calculate the value at time 6, starting from present_value
present_value * discount(___, ___)

Edit and Run Code